ME606 Digital Signal Processing, Melbourne Institute Of Technology, Australia

Master of Engineering (Telecommunications) School of Information Technology and Engineering

z-Transforms, Filters Concepts

DO YOU WANT TO EXCEL IN ME606 DIGITAL SIGNAL PROCESSING ASSIGNMENT - ORDER AT EXPERTSMINDS!

Question 1: Designing a low pass FIR filter using Windowed Fourier Series approach.

Answer: 1. Impulse Response

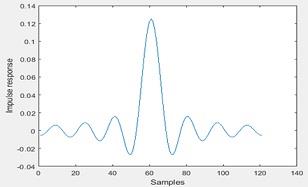
Figure 1 Impulse response of the low pass filter in rectangular window

Amplitude Spectrum

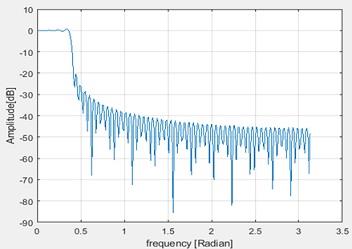
Figure 2 Frequency Spectrum

2. Filter frequency response at wp = pi/8 is shown below

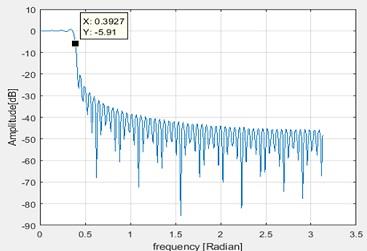
Figure 3 Filter frequency response at pi/8

This is measured as 5.91dB which is almost -6dB

Maximum ripple in the pass band is given below figure as 0.6821dB

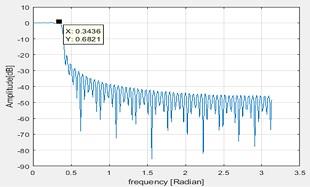
Figure 4 Maximum ripple in pass band

3. If the stopband starts at -20dB, the ratio of the transient band to the passband

Transient band = ws - wp

ws = -20dB dB

wp = -0.7093dB

Transient band = -20.7093dB

(Transient band)/(pass band) = (-20.7093)/(-0.7093) = 29.19dB

4. When m is 255 the impulse and amplitude response are below

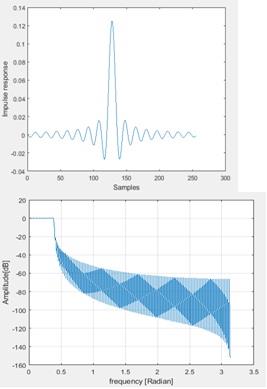
Figure 5 When the filter lenth is increased

a. If the stopband starts at -20dB, the ratio of the transient band to the passband

Transient band = ws - wp

ws = -20dB dB

wp = -0.5711dB

Transient band = -20.5711dB

(Transient band)/(pass band) = (-20.5711)/(-0.5711) = 36.02dB

b. Ripple in pass band is 0.7dB

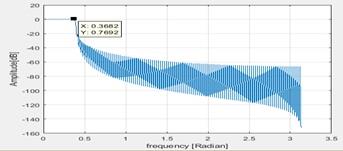
Figure 6 Maximum pass band

c. The effect of the filter length on the ripples and stopband attenuation: If the filter length is increased the ratio of the transition to the pass band is increased, whereas the stop band attenuation is -20dB itself.

5. Using the Hamming window the frequency response obtained is as below

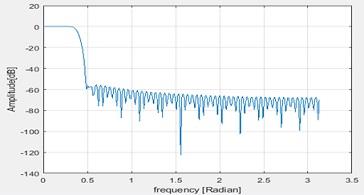
Figure 7 Hamming window

The stop band attenuation is -60dB. In the pass band the ripples are eliminated. This is the advantage of windowing.

Now if Hanning windowing is applied , the changes are as below

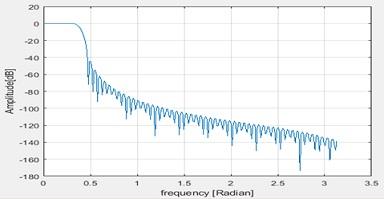
Figure 8 Hanning window

Here also the stop band attenuation is -60dB.

6. Now the pass band is changed to π/4

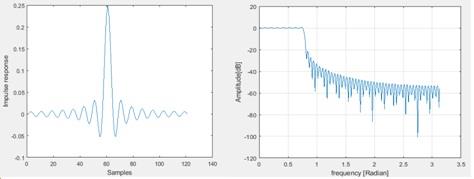
Figure 9 When the pass band is changed

The transition band is increased whereas the stop band remains same as -20dB itself and the pass band is changed with more ripples.

WORK TOGETHER WITH EXPERTSMIND'S TUTOR TO ACHIEVE SUCCESS IN ME606 DIGITAL SIGNAL PROCESSING ASSIGNMENT!

Question 2: Designing a bandpass FIR filter using Windowed Fourier Series approach

Answer: 1. The impulse response is as below

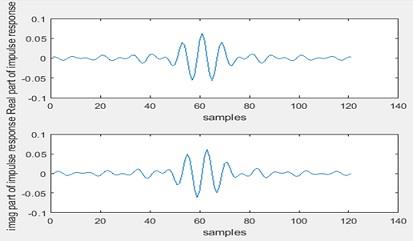
Figure 10 Response of the system

The amplitude spectrum is as below

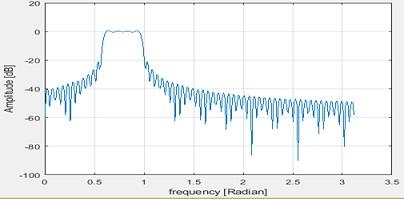
Figure 11 Frequency Spectrum

2. The pass band edges are given by

wp1 = -26.23dB , wp2 = -26.23dB and the frequency is almost 0.5 rad

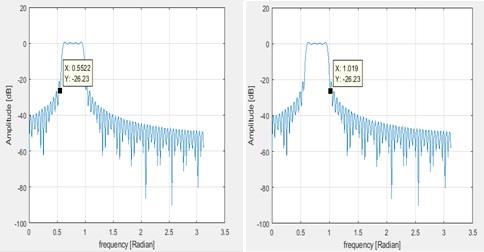
Figure 12 Pass band edges

The frequency at -6dB is as below

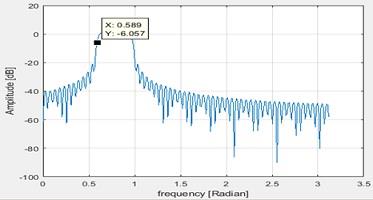
Figure 13 Frequency at -6dB

3. Maximum ripple in pass band is 0.7707dB

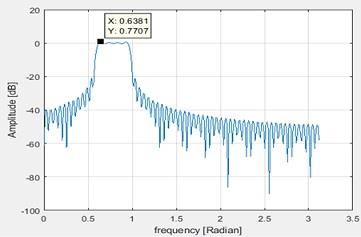
Figure 14 Maximum pass band

4. Now the pass band is changed to π/4

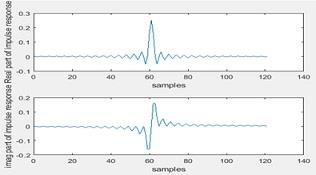
Figure 15 Impulse response

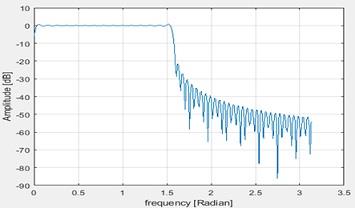
Figure 16 Fequency response

Wp1 = -2.788db and wp2 = -28.7dB

Here the pass band is more wider than the previous one which allows more frequencies to pass through.

ORDER NEW ME606 DIGITAL SIGNAL PROCESSING ASSIGNMENT AND GET 100% ORIGINAL SOLUTION AND QUALITY WRITTEN CONTENTS IN WELL FORMATS AND PROPER REFERENCING!

Question 3: Designing a band-stop FIR filter using Frequency sampling approach. In this section, you must write your own code to design a band stop filter using the knowledge you gained from the sections 1-1 and 1-2

Answer: 1. Mathlab code

wp = pi/8; % lowpass filter bandwidth

M = 121;

n = -(M-1)/2:(M-1)/2; % selection time window

h0 = (wp/pi)*sinc((wp/pi)*n); % truncated impulse response

h1 = h0.*rectwin(M)'; % windowing

h = h1.*exp(j*w0*n); % Lowpass to bandpass conversion

h2 = h1-h; % bandstop conversion

figure;

figure;plot(h2)

ylabel('Impulse response')

xlabel('Samples')

% spectrum

FFTsize = 512;

pxx = 20*log10(abs(fft(h2,FFTsize)));

fxx = (0:(FFTsize/2)-1)*(pi/(FFTsize/2));

figure;plot(fxx,pxx(1:FFTsize/2));ylabel('Amplitude [dB]');xlabel('frequency [Radian]');grid on

2. The frequency spectrum

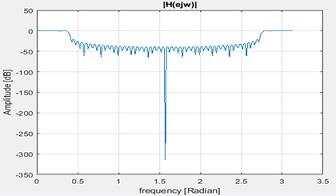
Figure 17 Frequency spectrum

3. Plot is as below

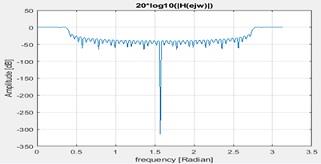
Figure 18 Spectrum

4. The amplitude at w=[w/4, 3w/4, w/2] are -37.14dB, -48.02dB and -42.26dB

5. The plot is as below

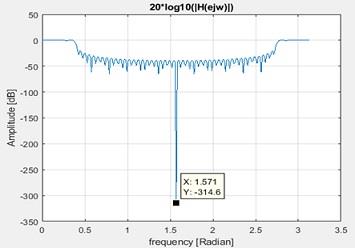
Figure 19 Spectrum when heading in included

MOST RELIABLE AND TRUSTWORTHY ME606 DIGITAL SIGNAL PROCESSING ASSIGNMENT HELP AND ASSESSMENT WRITING SERVICES AT YOUR DOORSTEPS!

Question 4: Designing a low pass FIR filter using Frequency sampling approach

Answer: 1. The responses are as below

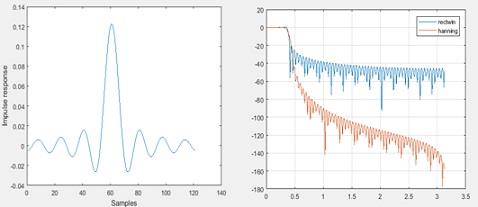
Figure 20 Both the spectrums

In the rectangular window the number of side lobes are higher. Hanning window minimizes the same.

2. The plot is

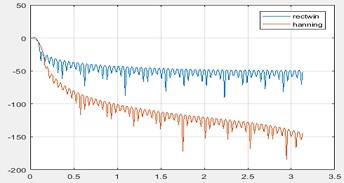
Figure 21 Spectrum

Section 2

3. Given that

H(Z) = ((1 - o.2Z^-1)/((1 - o.5Z^-1)(1 - o3Z^-1)))

We need to find the ROC

Re arranging this we get

(Z(Z - 0.2))/((Z - 0.5)(Z - 0.3))

By partial fraction solving we get

1 + (0.175/(Z - 0.5)) - (0.075/(Z - 0.3)) 

Taking inverse Z transform we get

∂(n) + 0.175 (0.5)ⁿ - 0.075(0.3)ⁿ

ROC will be n>o

4. The system is unstable as the poles lie on the left half.

5. It is a general form of filter

We can represent y(n) = ∑_(k=0)^M (b_k X(n-k)) - ∑_(k=0)^N (a_k Y(n-k))

On taking Z transform (Y(Z))/(X(Z)) = (bo+b1Z-1+ ---±BMZ-M)/(a0+a1Z±--±aNZ-N)

6. The values can be found out if we know the a,b, M and N values

7. The plot is

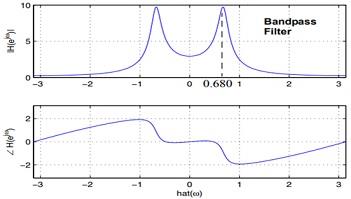
Figure 22 Various Figures

8. It is a band pass filter

9. The block diagram is

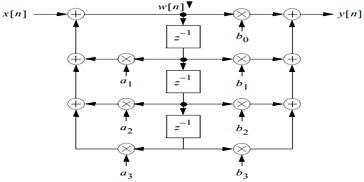
Figure 23 Block Diagam

10. y(n) = ∑_(k=0)^M (b_k X(n-k)) - ∑_(k=0)^N (a_k Y(n-k))

11. The plot is

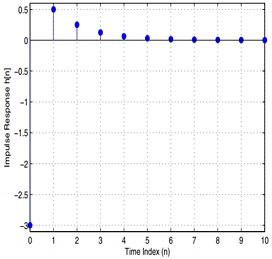
Figure 24 Impulse response

Section 3 Filtering

12. The plot os

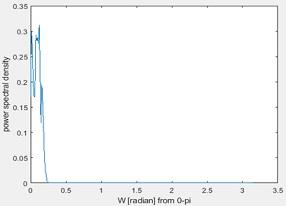
Figure 25 Power spectral density

It is the power spectral density estimate.

13. The plot is

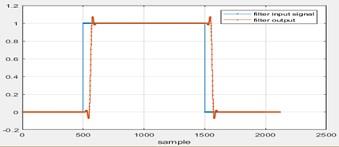
Figure 26 Filter characteristics

Delay by 0.099 compared to input.

Receive quality Melbourne Institute Of Technology, Australia assignment help and online tutor service for its major courses and units, like:

• ME503 - Telecommunication System Engineering Assignment Help
• ME700 - Industry Experience Assignment Help
• ME603 - Project Assignment Help
• ME601 - Telecommunication Modeling and simulation Assignment Help
• ME602 - Mobile and Satellite Communication Systems Assignment Help
• ME501 - Professional Engineering Practice Assignment Help
• MN605 - Enterprise Network Design Assignment Help
• ME693 - Software-Defined Radio Communication Assignment Help
• MN503 - Overview of Internetworking Assignment Help
• MN506 - System Management Assignment Help