Unit 35 Further Analytical Methods for Engineers Assignment - BTEC Level 5 HND Diploma in Engineering

Assignment - Analyse, Model & Solve Engineering Problems using First Order Diff. Equations

Learning outcomes -

• Analyse engineering problems and formulate mathematical models using first order differential equations
• Solve first order differential equations using analytical and numerical methods
• Analyse engineering problems and formulate mathematical models using second order differential equations
• Solve second order homogeneous and non-homogenous differential equations.
• Apply first and second order differential equations to the solution of engineering situations.

Purpose of this assignment - The purpose of this assignment is to allow you the opportunity to display your knowledge and capability of solving Differential Equations and to provide evidence on how you may formulate and solve them.

GET ASSURED A++ GRADE IN EACH UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT ORDER - ORDER FOR ORIGINALLY WRITTEN SOLUTIONS!

Task 1

Whilst testing the resistance of a copper conductor in your test rig, you observe that the rate of change of its resistance as temperature changes is equal to a constant (the temperature coefficient of resistance, which is 3.9 × 10^-3 for copper) multiplied by its current resistance.

(a) Formulate a first-order Differential Equation to describe this situation.

Solution: dR/dT = k x R

R = resistance

T = temperature

K = constant

(b) Given the following observational data about your conductor, solve the differential equation to find a formula for its resistance at a given temperature. At 0^oC, the resistance of the component is 50Ω.

Solution: dR/R = k dT

log R = kT + c

c = contant of integration

At 0 degree Celsius, R = 50 ? (given)

Log 50 = 0 + c

C = log 50

Log R = kT + log 50

(c) When the conductor's resistance exceeds (R=58Ω) it causes problems with the system's operation. Using your equation, find out the temperature at which it reaches the system.

Solution: R = 58 ?

Log 58 = kT + log 50

T = log 58 - log 50 / k = log(58/50)/k degree celsius

NO PLAGIARISM POLICY - ORDER NEW UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT & GET WELL WRITTEN SOLUTIONS DOCUMENTS WITH FREE TURNTIN REPORT!

Task 2 - The equation of motion of a train is given by mdv/dt = mk(1-e^-t)-mcv, where vis the speed, t is the time and m, k and c are constants. Determine the speed v given v=0 at t=0?

Solution: Equation of motion: mdv/dt = mk(1-e-t)-mcv

v = speed,

t = time

m, k and c = constants.

Given: v=0 at t=0

m dv/dt + mcv = mk (1 - e^-t)

dv/dt + cv = k (1 - e^-t)

Integrating factor = e^(ct)

v e^(ct) = Integration (e^(ct) k (1 - e^-t))

v e^(ct) = k (e^(ct) / c - e^(c-1)t / c-1) + c1

c1 = constant

c1 = k (1/c-1 - 1/c)

v e^(ct) = k (e^(ct) / c - e^(c-1)t / c-1) + k (1/c-1 - 1/c)

v = k (1 / c - e^(-1)t / c-1) + k e^(-ct) (1/c(c-1))

ENDLESS SUPPORT IN UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENTS WRITING SERVICES - YOU GET REVISED OR MODIFIED WORK TILL YOU ARE SATISFIED WITH OUR UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT HELP SERVICES!

Task 3 - A mathematical equation you are trying to solve has produced the differential equation dy/dx = 6x + 3y, with the conditions y=6 when x=0, you are only interested in it over a small range from x = 0 to x = 3 and do not want to invest the time necessary to properly solve it as you do not need an exact relationship.

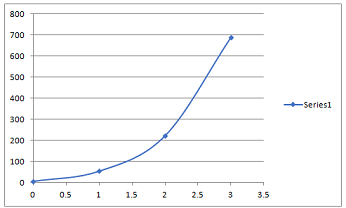
(a) Either manually or electronically apply Euler's method to this equation and draw a graph of the approximate solution over the required range.

Solution: Euler's Method: Y1 = y0 + h (y')0

X0 = 0, y0 = 6, (y')0= 18

Y1 = y0 + h (y')0 = 6 + 1 x 18 = 24

X0 = 1, y0 = 24, (y')0 = 6 + 3 x 24 = 78

Y1 = 24+78 = 102

X0 = 2, y0 = 102, (y')0 = 12 + 3 x 102 = 318

Y1 = 102+318 = 420

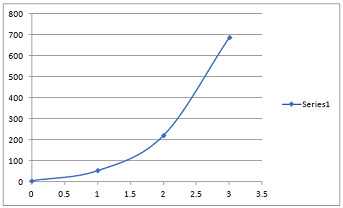
(b) Using your workings from the previous part where necessary, apply the Euler-Cauchy method to the same range and provide the resulting graph.

Solution: Euler-Cauchy method

Yc1 = y0 + h/2 [(y')0 + f(x1,yp1)]

Yc1 = 6 + ½ [18 + 6x1 + 3x 24] = 54

Yc2 = y1 + h/2 [(y')1 + f(x2,yp2)]

Yc2 = 24 + ½ [78 + 6 x 2 + 3 x 102] = 222

Yc3 = y2 + h/2 [(y')2 + f(x3,yp3)]

Yc3 = 102 + ½ [318 + 6 x 3 + 2 x 420] = 690

(c) Finally, apply the Runge-Kutta method and compare your three results, analysing their accuracy and time-efficiency.

Solution: Runge-Kutta Method

yn+1 = yn + h/6 (k1 + 2 k2 + 2 k3 + k4)

K1 = f(xn,yn)

K2 = f(xn+ h/2,yn + hk1/2)

K3 = f(xn + h/2,yn + hk2/2)

K4 = f(xn+h,yn+hk3)

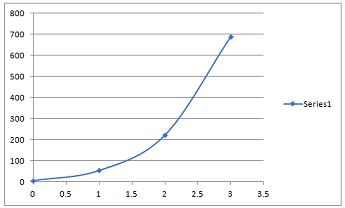
k1 = f(x0,y0) = 6 x 0 + 3 x 6 = 18

K2 = f(x0 + ½, y0 + 18/2) = 6/2 + 3 x 15 = 48

K3 = f(1/2, 6+24) = 93

K4 = f (1, 6+93) = 303

Y1 = 6 + 1/6 (18 + 2 x 48 + 2 x 93 + 303) = 106.5

X1 = 1, y1 = 106.5

k1 = f(x1,y1) = 6 x 1 + 3 x 106.5 = 325.5

K2 = f(3/2, 106.5+ 325.5/2) = 816.75

K3 = f(3/2, 106.5+816.75/2) = 1553.625

K4 = f (2, 106.5+1553.625) = 4992.375

Y2 = 106.5 + 1680.9 = 1787

k1 = f(2,1787) = 5373

K2 = f(5/2, 1787+ 2686.5) = 13435.5

K3 = f(5/2, 1787+6717.75) = 25529.25

K4 = f (3, 1787+25529.25) = 81966.75

Y3 = 1787 + 17803.7 = 19590.7

Real Calculation:

dy/dx - 3y = 6x

Y e^-3x = 6 (-x/3 e^-3x -1/9 e^-3x) + c

C = 6.67

Y = -2x -0.67 + 6.67 e^3x

Comparison:

We find that accuracy as well as time is maximum for Runge Kutta Method.

We find that accuracy as well as time is minimum for Euler's Method.

HELPING STUDENTS TO WRITE QUALITY UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT AT LOW COST!

Task 4 - Another part of your system involves an oscillating mass which may be looked at as a simple harmonic oscillator.

(a) Taking the given values Newton's Law (F_total = m (d²x/dt²)), Hooke's Law (F_spring = -kx) and the formula for a damping force on an oscillating mass (F_damp = -c dx/dt) formulate a second-order differential equation to describe this behaviour, given that the mounting spring has a spring constant k = 201, your damping mechanism produces a damping constant c = 500 and the oscillating mass has mass m = 0.45kg.

Solution: F_total = F_spring + F_damp

Md²x/dt² = -kx -c dx/dt

Md²x/dt² + kx + c dx/dt =0

0.45 d²x/dt² + 500 dx/dt + 201x =0

This is the required second-order differential equation.

(b) Solve this differential equation to find an expression for the position of your oscillator at any given time during its motion, (i.e. x(t)=[function]), given that when t=0 our mass begins with an offset of x=-0.5m, and is also static (dx/dt=0).

Solution: 0.45 d²x/dt² + 500 dx/dt + 201x =0

0.45 D2 + 500 D + 201 = 0

D = - 0.4, -1110.7

X = A e -0.4t + B e -1110.7t

At t=0, x = -0.5,

-0.5 = A+B

Dx/dt = -0.4 A e -0.4t - 1110.7 B e -1110.7t

0 = -0.4 A - 1110.7 B

Solving, A = -0.5, B = 0.00018

X = -0.5 e -0.4t + 0.00018 e -1110.7t

(c) Using your equation, find the position of the mass at time t=0.5.

Solution: X = -0.5 e^-0.4t + 0.00018 e^-1110.7t

X = -0.5 e^-0.4x0.5 + 0.00018 e^-1110.7x0.5 = - 0.5 x 0.82 + 0.00018 x 0 = -0.41

GET READYMADE UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT SOLUTIONS - 100% PLAGIARISM FREE WORK DOCUMENT AT NOMINAL CHARGES!

Task 5 - An oscillating LCR circuit is used in one of the systems you have been assigned. Its circuit is comprised of a Resistor of R=100Ω, an Inductor of L=0.5H and a capacitor of C=11mF.

(a) Given that it outputs a voltage of V=10sin(3t), using your knowledge of electronic circuits (sum of voltage drops=total voltage) formulate a differential equation to describe the system's behaviour in terms of current.

Solution: d²I/dt² + R/L di/dt + 1/LC i = 30 cos (3t) / 0.5

d²I/dt² + 200 di/dt + 181.82 i = 60 cos (3t)

This is the required differential equation.

(b) By solving this equation, find the relationship between Current (I) and time (t) given that I=0 at t=0 and I=0 at t=3s.

Solution: CF:

D² + 200 D + 181.82 = 0

D = -0.9, -199.1

I = A e-0.9t + B e-199.1t

PI:

I = 1/ D² + 200 D + 181.82 ( 60 cos 3t)

Put D² = -3x3 = -9

1/ 200 D+172.82 (60 cos 3t) = 2.5 (172.82-200D) x 60 cos 3t micro A

= 25 ( 172.82 x 6 cos 3t + 600 x 6 sin 3t)

= 25923 cos 3t + 90000 sin 3t

Total current, i(t) = A e^-0.9t + B e^-199.1t + 25923 cos 3t + 90000 sin 3t

At t=0,

0 = A+ B - 15000

A + B = 25923

At t = 3s,

0 = A e^-0.9x3 + B e^-199.1x3 + 25923 cos 3x3 + 90000 sin 3x3

0.067 A + 0 + 4320.5 x 0.412 - 15000 (-0.91) = 0

A = (-1780 - 13650)/0.067 = -2.30298.5

B = 15000 - A = 245298.5

i(t) = -2.30298.5 e-0.9t + 245298.5 e-199.1t + 25923 cos 3t + 90000 sin 3t

(c) Using this relationship, find the Current at time t=850ms.

Solution: I = -2.30298.5 e^-0.9x0.85 + 245298.5 e^-199.1x0.85 + 25923 cos 3 x 0.85 + 90000 sin 3 x 0.85

= - 1.072 +0 + 2409.47 + 12450.8 = 14859.2 micro A = 0.0149 A

MOST RELIABLE AND TRUSTWORTHY UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT HELP & HOMEWORK WRITING SERVICES AT YOUR DOORSTEPS!

Task 6 - Evaluate how different models of engineering systems using first and second order differential equations solve engineering problems for Tasks 1,2,4 and 5 above.

Solution: Different models of engineering systems using first and second order differential equations solve engineering problems.

The first case is variation of Resistance w.r.t. Temperature.

dR/dT = k x R

It is first order differential equation.

The second case represents equation of motion.

dv/dt + cv = k (1 - e^-t)

It is first order differential equation.

The case in Q4 is that of Simple Harmonic Oscillator.

Md²x/dt² + kx + c dx/dt =0

It is second order differential equation.

The case in Q5 is RLC Oscillator.

d²I/dt² + R/L di/dt + 1/LC i = 10 sin (3t)

It is second order differential equation.

SAVE DISTINCTION MARKS IN EACH UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT WHICH IS WRITTEN BY OUR PROFESSIONAL WRITER!

Task 7 - Critically evaluate first and second order differential equations when generating the solutions to engineering situations using models of engineering systems for Tasks 1,2,4 and 5 above and justify your conclusions by validation with alternative techniques e.g. use of computer programs or other external tools.

Solution:

Question 1: dR/dt = kR

Take k=1.

T=0 and R=50.

MATLAB Code:

syms r(t)

ode = diff(r,t) == r

cond = r(0) == 50

rSol(t) = dsolve(ode,cond)

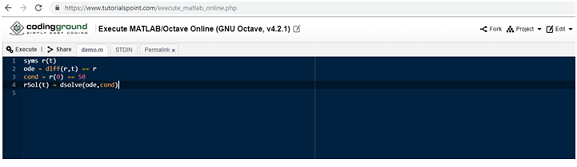
Same result is obtained.

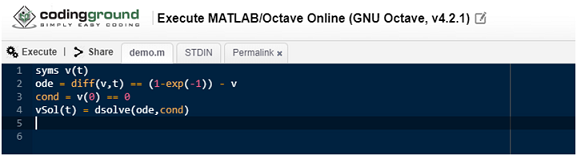
Question 2:

MATLAB Code:

syms v(t)

ode = diff(v,t) == (1-exp(-1)) - v

cond = v(0) == 0

vSol(t) = dsolve(ode,cond)

4) 0.45 d²x/dt² + 500 dx/dt + 201x =0

MATLAB Code:

syms x(t)

ode = 0.45*diff(x,t,2)+500*diff(x,t)+201x == 0;

xSol(t) = dsolve(ode)

5) d²I/dt² + 200 di/dt + 181.82 i = 10 sin (3t)

MATLAB Code:

syms I(t)

ode = 1*diff(i,t,2)+200*diff(i,t)-i == 0;

iSol(t) = dsolve(ode)

HIRE PROFESSIONAL WRITER FROM EXPERTSMINDS.COM AND GET BEST QUALITY UNIT 35 FURTHER ANALYTICAL METHODS FOR ENGINEERS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES!

Acquire best BTEC Level 5 HND Diploma in Engineering Assignment Help Services at Expertsminds for its related courses and units, such as:

• Unit 1: Analytical Methods for Engineers Assignment Help
• Unit 2: Engineering Science Assignment Help
• Unit 3: Project Design, Implementation and Evaluation Assignment Help
• Unit 4: Mechanical Principles Assignment Help
• Unit 5: Electrical and Electronic Principles Assignment Help
• Unit 6: Health, Safety and Risk Assessment in Engineering Assignment Help
• Unit 7: Business Management Techniques for Engineers Assignment Help
• Unit 8: Engineering Design Assignment Help
• Unit 9: Manufacturing Planning and Scheduling Principles Assignment Help
• Unit 10: Manufacturing Process Assignment Help
• Unit 11: Supply Chain Management Assignment Help
• Unit 12: Material Handling Systems Assignment Help