Semiconductor Physical Properties Assignment Questions -

ARE YOU LOOKING FOR RELIABLE SEMICONDUCTOR PHYSICAL PROPERTIES ASSIGNMENT HELP SERVICES? EXPERTSMINDS.COM IS RIGHT CHOICE AS YOUR STUDY PARTNER!

Question 1 - In an experiment, the current through and the voltage across the opposite faces of three specimen blocks of material, each 1 cm³, was measured using the circuit of FIGURE 1. Use the results of the experiment, given in the table below, to classify each material as insulator, conductor or semiconductor.

Answer - It is given in the question the voltage and current values of three specimens as follows

The length breadth and width of the material are 1cm each.

To check the given materials are insulators, conductors and semiconductors we can calculate the resistivity.

Resistivity ρ = RA/l

We know R = V/I

A = 1cm² and length = 1cm

So

Based on these values

DO YOU WANT TO EXCEL IN SEMICONDUCTOR PHYSICAL PROPERTIES ASSIGNMENT - ORDER AT EXPERTSMINDS!

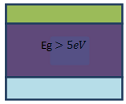
Question 2 (i) - Sketch and label energy-band diagrams of a metal, an insulator and a semiconductor and give approximate values of the energy gap where appropriate.

Answer - Energy band diagram

1 eV = 1.6 × 10^-19J

Question 2 (ii) - The three graphs of FIGURE 2 show how the resistivities of metals, insulators and intrinsic semiconductors vary over a small temperature range. Explain the shape of the graphs in terms of the energy-band theory of electrons in solids.

Answer - We can explain as follows

HIRE PROFESSIONAL WRITER FROM EXPERTSMINDS.COM AND GET BEST QUALITY SEMICONDUCTOR PHYSICAL PROPERTIES ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES!

Question 3 (i) - Determine the current flowing through a 1 cm cube of pure silicon when a potential of 1 V is applied across opposite faces (FIGURE 3(a)) if the number density of hole-electron pairs in the cube 1.56 x 10¹⁶ m^-3.

Answer - We need to determine the current flowing

As we know the resitivity is ρ = RA/l

R = ρl/A

V/I = ρl/A = l/Aσ = l/Aqdesity

= (1×10^-2)/(1×10^-6 × 1.6×10^-19 × 1.56×10¹⁶)

I = (1×10^-6 × 1.6×10^-19 × 1.56×10¹⁶)/(1×10^-2)

I = 2.496×10^-7A

= 0.2496µA

Question 3 (ii) - A lamp is now allowed to shine upon one face of the cube as shown in FIGURE 3(b). This has the effect of generating hole-electron pairs at the surface of the exposed face and so raising the number densities of the carriers at that surface to a value of 1 x 10²⁰ carriers m^-3. For the polarities of external connections as shown, calculate the change in hole current due to the effects of the light.

Answer - We need to determine the current flowing

As we know the resitivity is ρ = RA/l

R = ρl/A

V/I = ρl/A = l/Aσ = l/Aqdesity

= (1×10^-2)/(1×10^-6 × 1.6×10^-19 × 1×10²⁰)

I = (1×10^-6 × 1.6×10^-19 × 1×10²⁰)/(1×10^-2)

I = 1.6×10^-3 A

= 1.6mA

Question 3 (iii) - If the polarity of the supply is now reversed, calculate the change in electron current due to the light. Again, assume a linear density gradient.

Answer - If the polarity is reversed then the current will change its direction as -1.6mA.

MOST RELIABLE AND TRUSTWORTHY SEMICONDUCTOR PHYSICAL PROPERTIES ASSIGNMENT HELP & HOMEWORK WRITING SERVICES AT YOUR DOORSTEPS!

Question 4 - Use the Fermi-Dirac probability function

p(W) = (1+ exp((W-W_F)/kT))^-1

to calculate, for pure silicon at a temperature of 27^oC, the probability of:

(a) an electron just being at the bottom of the conduction band

Answer - Electron at the bottom of conduction band

w-w_F = 0

so exp[(w-w_F)/KT] = 1

p(w) = (1+1)^-1 = ½5

(b) A hole just being at the top of the valence band.

Answer - Hole at the top of conduction band

w-w_F = 0

so exp[(w-w_F)/KT] = 1

p(w) = (1+1)^-1 = 1/2

Question 5 - A silicon 'chip' has the dimensions 8 x 2 x 2 mm.

(i) Calculate its resistance as measured between the square faces, assuming it is of intrinsic material. Take the carrier number density of hole-electron pairs as 1.5 x 10¹⁶ m^-3 at room temperature.

Answer - We need to calculate the resistance

Given that a pure si at absolute temperature

So σ = q(μn + μp)ni

We know the values of μn + μp = 0.15 + 0.05 = 0.2

Now σ = 1.6×10^-19 × 0.2×1.5×10¹⁶

= 0.48×10^-3

Now ρ = (σ)^-1

ρ = 2083

R = ρl/A = (2083×8×10^-3)/(16×10^-6) = 10.4MΩ

(ii) Estimate its resistance at 10^oC above room temperature.

Answer - Resistance at 10^oC above room temperature

Almost same as 10.4MΩ because the si sample is not doped at this temperature.

(iii) Calculate the resistance, again across the square faces and at room temperature, if the 'chip' is now uniformly doped with aluminium, so that one in every 10⁷ atoms is an impurity atom (a cubic metre of silicon contains about 5 x 10²⁸ atoms). Also apply the 'law of mass action' to calculate the minority carrier density.

Answer - σ = q(μnno + μppn)

Given that n₀ = 5×10²⁸

Now p_o = (n_i²)/n₀ = 5120

Now σ = 1.6×10^-19[0.15×5×10²⁸ + 0.5×5120]

= 12×10⁸

Now ρ = (σ)^-1

ρ = 0.0833×10^-8

R = ρl/A = (0.0833×10-8×8×10^-3)/(16×10^-6) = 0.042×10⁵Ω

(iv) Estimate the resistance of the doped 'chip' at 10^oC above room temperature.

Answer - When temperature is greater than room temperature the resistance will have slight variations.

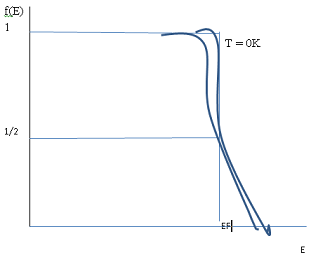
(v) Sketch, on the same axes, the energy/probability distribution curve for n-type silicon at two temperatures T₁ and T₂ (where T₂ > T₁) to show the effect of temperature upon the position of the Fermi level.

Answer - The diagram is as below

Acquire our Teesside University course help and assignment help services for various related courses such as: -

• Analytical Methods for Engineers Assignment Help
• Engineering Science Assignment Help
• Electrical and Electronic Principles Assignment Help
• Project Assignment Help
• Applications of Pneumatics and Hydraulics Assignment Help
• Digital and Analogue devices and circuits Assignment Help
• Distributed Control Systems Assignment Help
• Electrical machines Assignment Help
• Engineering Applications Assignment Help
• Mechatronics Systems Principles Assignment Help