Partial Differential Equation Assignment Help

1. A climate scientist makes the following observations on the weather in Ballarat in winter:

i There are never two consecutive days of nice weather.

ii Following a nice day, there are equal probabilities (i.e. 1) of having either a rainy day or a windy day.

iii Following a rainy day or a windy day, the probability of having the same weather the next day is 1, and the probability of having a nice day is 1.

a) What is the state space of this process?

b) Write down the Markov chain modelling the weather in Ballarat according to these ob-servations.

c) Show that this is a regular Markov chain.

d) Find the equilibrium (stationary) distribution of the Markov chain.

e) In the 3 months (90 days) of winter, how many days of nice weather can be expected? 1+1+2+2+1 marks

2. Let u(x, t) be a function of two variables which satisfies the following partial differential equation:

N u - + - = 3x Ox x

a) Solve to determine u. (Note that the PDE contains only u, derivatives of u, and functions of x.

b) Find the solution which satisfies u(1, t) = sin2 t. c) Find any non-constant solution to the following partial differential equation: 02u 1 Ou 0 Ox0y x Oy

3. Rewrite the third-order differential equation cos tym(t) + sy (t) - ety(t) = 2t as a system of first-order differential equation.

No Plagiarism Policy – Order New Partial Differential Equation Assignment Help solution & Get Well Written Solutions Documents with Free Turnitin Report!

1)

a) State space for this process is shown below :

State Space = {nice day, rainy day, windy day}

b)

The Markov chain Modeling of the weather in Ballarat according to these observations is shown below :

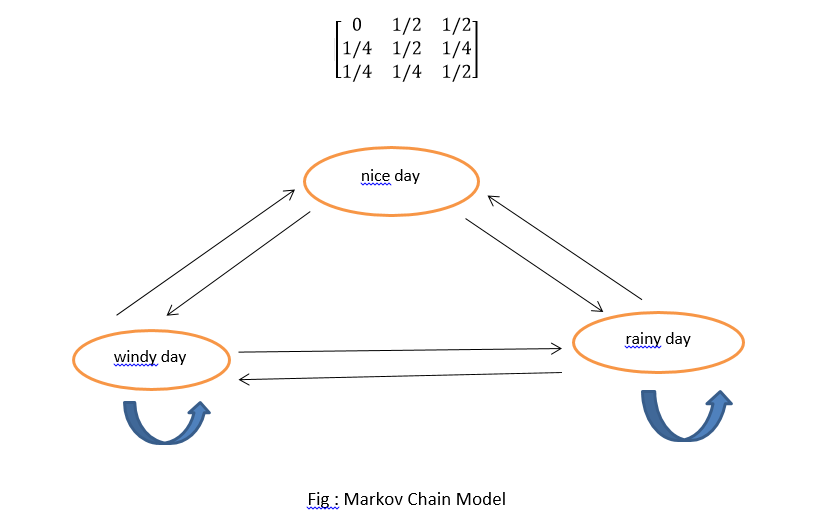
C)

So to show regular markov matrix it should be P²=P.

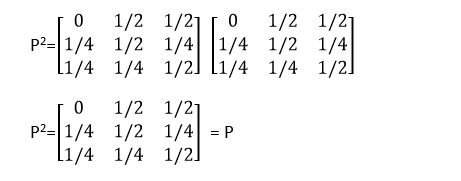
Therefore As Matrix multiplication gives P so it is a regular markov matrix.

d)

The equilibrium distribution of the markov chain is as below :

S =[ 1/2  1/4  1/4  ]

Since,

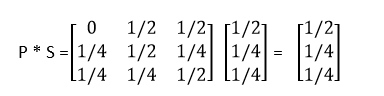
Therefore as  P * S gives S itself So it is equilibrium distribution.

e)

Total number of observations of days in weather = 90 days

Now,

Probability = favorable observations/ total number of observations

Probability of nice days = 1/4

So

1/4 = number of expected nice days/90

number of expected nice days = 1/4*90 = 22.5

So the numbers of expected nice days are 23 days.

2)

The differential equation given :

du/dx + u/x  = 3x

a)

?u/?x + u/x = 3*x

Multiplying x with whole equation on both sides gives

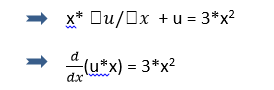
Integrating both sides

u*x = 3*x³/3

 So the answer is   u = x² .

b)

Now putting U(1,t) in the above solution u = x²  gives  as

As U(1,t) = sin²t

1 = sin²t

t = 90^o , -90^o

c)

Given :

?²u/?x?y + (1/x) *?u/?y = 0

Now rearranging the equation

  - ?²u/?x?y = (1/x) *?u/?y

Integrating on both sides with respect to x and then with y we get

u = - (log x)*y

3)

given:

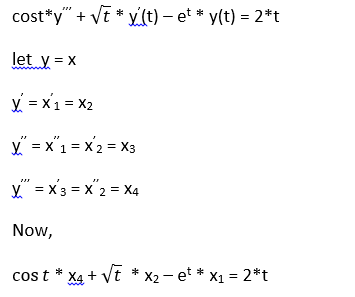
Y = AX

x₁ = x

        x^’₁ = x₂

        x^’₂ = x₃

        x^’₃ = x₄

             x^’₄ = (2*x₁ + e^t *x₁ –  * x₂)/

So the third order differential equation is written as a system of first order differential equation as :

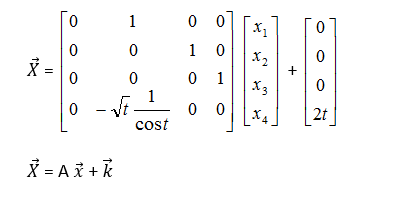
Endless support in Partial Differential Equation Assignment Help solution Writing Services - You get revised or modified work till you are satisfied with our assignment help services!