ORDER NEW COPY OF LINEAR PROGRAMMING ASSIGNMENT & GET HIGH QUALITY SOLUTIONS FROM SUBJECT'S TUTORS!
Question 1. Solve the following LP to obtain the optimal solution.
Maximize Z = 5X1 + 3X2 + 7X3
S.T. 4X1 + 3X2 + 2X3 ≤ 50
2X1 + 3X2 + X3 ≤ 30
3X1 + 2X2 - X3 ≤ 15
X1, X2, X3 ≥ 0
Answer:
The following is the basic table:
|
|
C
|
5
|
3
|
7
|
0
|
0
|
0
|
|
|
|
|
Coefficient
|
Basics
|
X1
|
X2
|
X3
|
S1
|
S2
|
S3
|
|
RHS
|
RATIO
|
|
0
|
S1
|
4
|
3
|
2
|
1
|
0
|
0
|
|
50
|
25
|
|
0
|
S2
|
2
|
3
|
1
|
0
|
1
|
0
|
|
30
|
30
|
|
0
|
S3
|
3
|
2
|
-1
|
0
|
0
|
1
|
|
15
|
-15
|
|
|
Z
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
C-Z
|
5
|
3
|
7
|
0
|
0
|
0
|
|
|
|
The z value is the sum product of individual columns and the coefficient column.
The values in C-Z column is not zero. So, we find the maximum of C-Z value which is 7 and X3 becomes the entering variable. The ratio is calculated by dividing RHS by the pivot column i.e. X3 values.
The negative ratio is neglected and the next minimum value is taken which is 25 and hence S1 is the leaving variable.
The new table is as follows:
|
|
C
|
5
|
3
|
7
|
0
|
0
|
0
|
|
|
|
Coefficient
|
Basics
|
X1
|
X2
|
X3
|
S1
|
S2
|
S3
|
|
RHS
|
|
7
|
X3
|
2
|
1.5
|
1
|
0.5
|
0
|
0
|
|
25
|
|
0
|
S2
|
0
|
1.5
|
0
|
-0.5
|
1
|
0
|
|
5
|
|
0
|
S3
|
5
|
3.5
|
0
|
0.5
|
0
|
1
|
|
40
|
|
|
Z
|
14
|
10.5
|
7
|
3.5
|
0
|
0
|
|
|
|
|
C-Z
|
-9
|
-7.5
|
0
|
-3.5
|
0
|
0
|
|
|
S1 is replaced by X3 and the value of X3 row is now 4/2, 3/2,2/2,1/2,0/2,0/2.
The second row is now (old values - 1*(the new line of X3))
The third row is now (old value - (-1* new line of X3))
The new Z and C-Z values are calculated. Now, C-Z values are less than zero. Hence, the solution is X1 = 0, X2=0 and X3=25.
The maximum value of Z = 25*7=175
ARE YOU LOOKING FOR RELIABLE LINEAR PROGRAMMING ASSIGNMENT HELP SERVICES? EXPERTSMINDS.COM IS RIGHT CHOICE AS YOUR STUDY PARTNER!
Question 3. Find the starting tableau for the following Transportation problem using Vogel's Method.
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
|
Q
|
|
S1
|
6
|
8
|
4
|
3
|
9
|
|
30
|
|
S2
|
4
|
3
|
5
|
7
|
4
|
|
20
|
|
S3
|
9
|
5
|
7
|
4
|
2
|
|
25
|
|
S4
|
7
|
4
|
6
|
9
|
5
|
|
35
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
|
15
|
|
|
|
|
|
|
|
|
|
|
Q
|
20
|
30
|
40
|
30
|
30
|
|
|
Answer:
The following is the solution:
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3
|
9
|
30
|
4-3=1
|
|
S2
|
4
|
3
|
5
|
7
|
4
|
20
|
4-3=1
|
|
S3
|
9
|
5
|
7
|
4
|
2
|
25
|
4-2=2
|
|
S4
|
7
|
4
|
6
|
9
|
5
|
35
|
5-4=1
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
5-4=1
|
|
Additional supply
|
0
|
0
|
0
|
0
|
0
|
25
|
0-0=0
|
|
Q
|
20
|
30
|
40
|
30
|
30
|
150
|
|
|
Column penalty
|
4-0=4
|
3-0=3
|
4-0=4
|
3-0=3
|
2-0=2
|
|
|
First the total of demand = 150 whereas total of supply = 125.
Hence, to balance, we add the additional supply unit for 25 units and the cost associated is zero.
Then, we calculate the row penalty which is the difference between the minimum value in a row and the corresponding next higher number and the column penalty which is the difference between the minimum value in a column and the corresponding next higher number.
4 is the maximum of all the penalties, but there are two columns with same. So, we assign to the one with the least cost.
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3
|
9
|
30
|
4-3=1
|
|
S2
|
4
|
3
|
5
|
7
|
4
|
20
|
4-3=1
|
|
S3
|
9
|
5
|
7
|
4
|
2
|
25
|
4-2=2
|
|
S4
|
7
|
4
|
6
|
9
|
5
|
35
|
5-4=1
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
5-4=1
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
20
|
30
|
15
|
30
|
30
|
|
|
|
Column penalty
|
6-4=2
|
4-3=1
|
5-4=1
|
4-3=1
|
4-2=2
|
|
|
The supply of 25 units is supplied as it is min(40,25) and hence, demand reduces to 40-25=15. Now, we don't take the additional supply row under consideration.
Again, we calculate the row and column penalty. Now, the maximum is 2. This time, we have 2 columns and 1 row with the penalty value of 2. Hence, we take with the least cost. Of all, the row S2 has the least cost. So, we assign it.
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3
|
9
|
30
|
4-3=1
|
|
S2
|
4
|
3
|
5
|
7
|
4
|
20
|
4-3=1
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4
|
6
|
9
|
5
|
35
|
5-4=1
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
5-4=1
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
20
|
30
|
15
|
30
|
5
|
|
|
|
Column penalty
|
6-4=2
|
4-3=1
|
5-4=1
|
5-3=2
|
5-4=1
|
|
|
Now, S3 is meeting demand of min(25,30) which I s25 and the row S3 strikes out with Q5 demand as (30-25=5). Again the row and column penalty are taken into consideration and the maximum value is 2 with two columns. D4 has the least cost.
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3(30)
|
9
|
0
|
-
|
|
S2
|
4
|
3
|
5
|
7
|
4
|
20
|
4-3=1
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4
|
6
|
9
|
5
|
35
|
5-4=1
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
7-4=3
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
20
|
30
|
15
|
0
|
5
|
|
|
|
Column
|
7-4=3
|
4-3=1
|
6-5=1
|
-
|
5-4=1
|
|
|
30 is supplied at D4 and hence, S1 row strikes out and the D4 column as well. Again, the row and column penalty are calculated and 3 is taken as the maximum penalty with one row and column having the same value. The one with least cost is D1 and min(20,20) which is 20. Both S2 and D1 is excluded.
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3(30)
|
9
|
0
|
-
|
|
S2
|
4(20)
|
3
|
5
|
7
|
4
|
0
|
-
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4
|
6(15)
|
9
|
5
|
20
|
5-4=1
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
7-4=3
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
0
|
30
|
0
|
0
|
5
|
|
|
|
Column
|
-
|
7-4=3
|
-
|
-
|
5-4=1
|
|
|
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3(30)
|
9
|
0
|
-
|
|
S2
|
4(20)
|
3
|
5
|
7
|
4
|
0
|
-
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4(20)
|
6(15)
|
9
|
5
|
0
|
-
|
|
S5
|
8
|
7
|
10
|
5
|
4
|
15
|
7-4=3
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
0
|
10
|
0
|
0
|
5
|
|
|
|
Column
|
-
|
7
|
-
|
-
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3(30)
|
9
|
0
|
-
|
|
S2
|
4(20)
|
3
|
5
|
7
|
4
|
0
|
-
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4(20)
|
6(15)
|
9
|
5
|
0
|
-
|
|
S5
|
8
|
7(10)
|
10
|
5
|
4
|
5
|
4
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
0
|
0
|
0
|
0
|
5
|
|
|
|
Column
|
-
|
-
|
-
|
-
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1
|
D2
|
D3
|
D4
|
D5
|
Q
|
Row penalty
|
|
S1
|
6
|
8
|
4
|
3(30)
|
9
|
0
|
-
|
|
S2
|
4(20)
|
3
|
5
|
7
|
4
|
0
|
-
|
|
S3
|
9
|
5
|
7
|
4
|
2(25)
|
0
|
-
|
|
S4
|
7
|
4(20)
|
6(15)
|
9
|
5
|
0
|
-
|
|
S5
|
8
|
7(10)
|
10
|
5
|
4(5)
|
0
|
-
|
|
Additional supply
|
0
|
0
|
0(25)
|
0
|
0
|
0
|
-
|
|
Q
|
0
|
0
|
0
|
0
|
0
|
|
|
|
Column
|
-
|
-
|
-
|
-
|
-
|
|
|
The final answer is as follows:
The minimum cost is (3*30)+(4*20)+(25*2)+(4*20)+(6*15)+(7*10)+(4*5)+(0*25)=480
EXPERTSMINDS.COM ACCEPTS INSTANT AND SHORT DEADLINES ORDER FOR LINEAR PROGRAMMING ASSIGNMENT - ORDER TODAY FOR EXCELLENCE!
Question 4. Solve the following Assignment problem using the Hungarian Method.
|
|
J1
|
J2
|
J3
|
J4
|
J5
|
|
W1
|
3
|
9
|
2
|
3
|
7
|
|
W2
|
6
|
3
|
5
|
8
|
6
|
|
W3
|
9
|
4
|
7
|
10
|
3
|
|
W4
|
2
|
5
|
3
|
2
|
4
|
|
W5
|
9
|
6
|
2
|
4
|
5
|
Answer:
The minimum value in each row is taken and all the values in the same row is subtracted.
In row 1, minimum value is 2
In row 2, minimum value is 3
In row 3, minimum value is 3
In row 4, minimum value is 2
In row 5, minimum value is 2
|
Rowwise
|
|
|
|
|
|
|
|
J1
|
J2
|
J3
|
J4
|
J5
|
|
W1
|
1
|
7
|
0
|
1
|
5
|
|
W2
|
3
|
0
|
2
|
5
|
3
|
|
W3
|
6
|
1
|
4
|
7
|
0
|
|
W4
|
0
|
3
|
1
|
0
|
2
|
|
W5
|
7
|
4
|
0
|
2
|
3
|
Now, the minimum value in column is taken and then the same is subtracted from each value in that column.
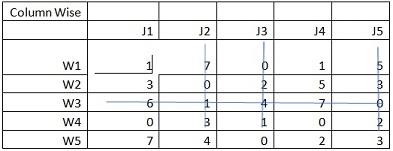
The blue lines indicate the minimum lines drawn to cover the zero values.
|
4 (number of lines) is not equal to 5 (order of the matrix)
|
|
So, add 1 to the intersection and subtract 1 from others
|
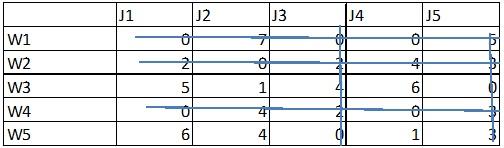
Now, the lines are drawn to cover the zero values in the minimum number of lines.
5 (number of lines) is not equal to 5 (order of the matrix).
Hence, the zero values are taken so that it is unique to each row and column.
The solution is as follows:
|
W1
|
J1
|
3
|
|
W2
|
J2
|
3
|
|
W3
|
J5
|
3
|
|
W4
|
J4
|
2
|
|
W5
|
J3
|
2
|
Question 5. Formulate the following problem as LP Model
The company's goal is to determine the quantities of each product which should be produced in order to achieve the highest profit. Define in detail the decision variables and form the objective function and all constraints of the problem.
Answer:
The three products are a = x units, b= y units and c = z units be produced by the company. The units x, y and z are the decision variables.
Revenue equation is as follows:
Revenue=142x+185y+224z
The cost is as follows:
Cost of raw material produce product a=(20+36+20+6)x=82x
Cost of raw material produce product b=(30+24+15+18)y=87y
Cost of raw material produce product a=(50+48+15+30)z=143z
The total cost is as follows:
Total cost=82x+87y+143z
The objective is to maximize profits:
Profit=Revenue-Total cost
Profit=142x+185y+224z-82x-87y-143z
Profit=60x+98y+81z
The constraints are as follows:
Demand constraint for a:x≤250
Demand constraint for b:y≤140
Demand constraint for c:z≤60
Raw material constraint for 1:2x+3y+5z≤1000
Raw material constraint for 2:3x+2y+4z≤1200
Raw material constraint for 3:4x+3y+3z≤1500
Raw material constraint for 4:x+3y+5z≤900
Thus, the following is the LP problem:
Maximise
z=60x+98y+81z
S.T.
x≤250
y≤140
z≤60
2x+3y+5z≤1000
3x+2y+4z≤1200
4x+3y+3z≤1500
x+3y+5z≤900
x,y,z≥0
DO WANT TO HIRE TUTOR FOR ORIGINAL LINEAR PROGRAMMING ASSIGNMENT SOLUTION? AVAIL QUALITY LINEAR PROGRAMMING ASSIGNMENT WRITING SERVICE AT BEST RATES!