ARE YOU LOOKING FOR RELIABLE FLUID MECHANICS ASSIGNMENT HELP SERVICES? EXPERTSMINDS.COM IS RIGHT CHOICE AS YOUR STUDY PARTNER!

Fluid Mechanics Assignment

Question 1: The velocity vector V at a point is given by 24i - 32j + 2k. Determine the resultant velocity.

Solution:

Given:
The velocity vector V at a point: 24i - 32j + 2k.
To find: Thee resultant velocity, R

The resultant Velocity can be found be:
The velocity vector can be rearranged and written as:

R = (24 -32 2)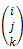

Now,

As the resultant is the sum of two or more vectors considering the second vector to be0i - 0j +0k.

The resultant velocity at the direction,
I: 24+0 = 24
J: -32+0 = -32
K: 2+0 = 2

ORDER NEW COPY OF FLUID MECHANICS ASSIGNMENT & GET HIGH QUALITY SOLUTIONS FROM SUBJECT'S TUTORS!

Question 2: Determine the coefficient of discharge for a Venturimeter given a differential head of 18.6 m of water. Assume that 4% of the differential head is lost between the inlet and throat.

Solution:

To find:
Cd, Coefficient of discharge.
Given:
Head, h: 18.6 m
Head loss: 4%: 0.04
Area: 1 m
Flow, Q: 5 m³/s (Assumed)

Discharge,
Q=AC_d √2gH
Where,
A is Area
C_d is discharge coefficient.
H is head
g is Acceleration due to gravity.

C_d=Q/(A √2gH)=5/((A(19.103)))=0.2617

The coefficient of discharge of the venturimetre is found to be 0.2617

SAVE TOP GRADE USING FLUID MECHANICS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM

Question 3: The diameters of a pipe are 16 cm and 24 cm at sections 1 and 2 respectively. The velocity of water flowing through the pipe is 5 m/sec at section 1. Determine the discharge through the pipe and also the velocity of flow at section 2

Solution: The diameters of a pipe are 16 cm and 24 cm at sections 1 and 2 respectively. The velocity of water flowing through the pipe is 5 m/sec at section 1. Determine the discharge through the pipe and also the velocity of flow at section 2

Given:
D1: 16 Cm = 0.16 m
D2: 24 Cm = 0.24 m
V1: 5 m/s

To find:
Velocity at section 2, V2: ?
Discharge, Q = ?

We know the formula:
Q1=Q2
Q1=V1 A1=Q2=V2 A2
Where,
Q1: Discharge at section 1
Q2: Discharge at section 2
V1: Velocity at section 1
V2: Velocity at section 2
V1 A1=V2 A2
V2= (V1 A1)/A2

Now,
A1 = Πr₁² = 0.020106 m²
A2 = Πr₂² = 0.04523 m²

Applying in V2 formula:
V₂= (5 (0.020106))/0.04523=2.222 m/s

The velocity at the section 2 is found to be 2.222 m/s

The Discharge,
Q=V1A1=0.10053 m³/s

GET BENEFITTED WITH QUALITY FLUID MECHANICS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM

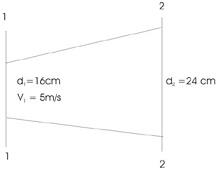
Question 4: A pipe of 45 cm diameter carrying water, branches into two other pipes of diameters 28 cm and 24 cm respectively. If the average velocity in the 45 cm pipe is 2.4 m/sec, find the flow rate in this pipe. Also determine the velocity in the 24 cm pipe if the average velocity in the 28 cm pipe is 2.0 m/sec.

Solution:

Given:
D1: 0.45 m
A1: 0.159043
D2: 0.28 m
A2: 0.06157
D3: 0.24 m
A3: 0.0452389
V1: 2.4 m/s
V2: 2 m/s

To find:

Discharge, Q = ?

Velocity at section 3, V3: ?

To find the discharge,

Q1 = Q2 + Q3

The discharge at pipe 1:

Q1= V1 A1

Q1=(2.4)(0.159043)=0.3817 m^3/s

To find velocity, V3:

Q1 = Q2 + Q3

Q1: 0.3817 m3/s

Q2 = V2 A2 = 0.12314 m3/s

0.3817 = 0.12314 + Q3

Q3 = 0.25856 m^3/s

Q3 = V3 A3

V3 = Q3/A3 = 0.25856/ 0.0452389

V3 = 5.7154 m/s

The velocity at the section 3 is found to be 5.7154 m/s

DO YOU WANT TO EXCEL IN FLUID MECHANICS ASSIGNMENT - ORDER AT EXPERTSMINDS!

Question 5: A fluid flow field is given by V=x³yi +y³zj-(3xyz+ yz³)k. Prove that it is a case of possible steady incompressible fluid flow. Calculate the velocity at the point (3, 2, 4).

Solution:

Given:
Fluid flow field: V=x³ yi+y³ zj-(3xyz+yz³ )k.

To find:
(i) To prove that it is a case of possible steady incompressible fluid flow.
(ii) To calculate the velocity at the point (3, 2, 4).

Answer:

For a steady state incompressible flow, the equation must be equal to 0 if the terms (I, j, k) = (0, 0, 0)

Applying: (I, j, k) = (0, 0, 0)

In Equation:V=x³ yi+y³ zj-(3xyz+yz³ )k.

V=x³ y(0)+y³ z(0)-(3xyz+yz³ )(0)=0

Thus the equation passes the Steady flow incompressible fluid criteria, hence it is a steady flow incompressible fluid.

(ii) To find the velocity at the point (3, 2, 4):

Applying the below values in equation V:

Let: (I, j, k = 1, 1, 1)

(x, y, z) = (3, 2, 4)

V=3³ (2)(1)+2³ (4)-(3(24)+2(4)³ )(1)=86-80=6 m/s

The velocity at the given point is found to be 6 m/s

DONT MISS YOUR CHANCE TO EXCEL IN FLUID MECHANICS ASSIGNMENT! HIRE TUTOR OF EXPERTSMINDS.COM FOR PERFECTLY WRITTEN FLUID MECHANICS ASSIGNMENT SOLUTIONS!