ORDER NEW COPY OF NUMBERED SETS AND REDUCTIONS ASSIGNMENT AND SECURE HIGHER MARKS!

Numbered Sets and Reductions Assignment

Question 1.
Numbered sets. Substantiate that sets are numbered:
a) Set Z3, consists of all three (a ,b, c), where a, b, c - integers;
b) Set GRAPHS, consists of all graphs G with final number (not endless) of vertices

Answer 1(A)
we know that the Z is the set of the integers and the set Z3 represents the set with basis or place 3.
An integer is positive if it is greater than zero and negative if it is less than zero. Zero is defined as neither negative nor positive. As given in question that a.b.c are integers , so it is proved that the following sets are numbered.

Answer 1(B)
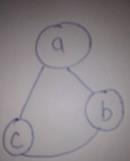
Consider G:V={a.b.c}
E={(a,b)(b,a)(a,c)(c,a)(b,c)(c,b)}

So the graph will be

NEVER BE CAUGHT IN PLAGIARISM, AVAIL NUMBERED SETS AND REDUCTIONS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM AND SAVE HIGHER MARKS!

Question 2.

Reductions. Look at the problem HALTING3, where input data consists of Turing Machine program M and three input strings x, y, z and HALTING3 (M, x, y, z), if M stops on each of these strings. Lets prove that HALTING3 ≤ HALTING, where HALTING - ordinary stop problem.

Answer:
Here, in given information,HALTING3 (M, x, y, z), contains three strings to be checked. And Halting one contains only a self introduced variable M in it.

For proving it
We take a function as such that HALTING3(M, w) and  (M', w') where M is an arbitrary ordinary TM, w is a string over the input alphabet of M, M' is a result after halting or operations, and w' is a result after checking of string set w={x,y,z} and M accepts w if and only if M' accepts w'. Given any M, let M' be the DMTM constructed in TM and let w' = f(w), where f is the function and part of w. now, we can see that the search containing three strings due to the large number of stops. And there is only a self variable M in it, the number of stops or halting will be minimum in comparison of HALTING3.

It will be due to large number of variable present in HALTING3 in comparison of HALTING.
So proved thatHALTING3 ≤ HALTING.

EXPERTSMINDS.COM GIVES ACCOUNTABILITY OF YOUR TIME AND MONEY - AVAIL TOP RESULTS ORIGINATED NUMBERED SETS AND REDUCTIONS ASSIGNMENT HELP SERVICES AT BEST RATES!

Question 3:

Algorithmic non resolvability.Lets prove that problems below cannot to be algorithmically solved:
a) A(M) = 1, if M - Turing Machine program and if M runs on empty input strings, Turing Machine stops and print 1.
b) B(M) = 1, if M - Turing Machine program and there does not have any input for string length 2, 4, 6, 8, on which M stops.
c) C(M, x, q) = 1, if M - Turing Machine program, x - input data, q - state. On input data x Turing Machine M somewhen comes into state q

Answer 3(a) :
if for any language or function A(M)=1. And there is an empty input string empty input string means that there is no available space or any available taps on turing that will accept the string. So when TM will start operation. Initially the search will end wnd will come to a default value or will print the default value as a result.

A Turing Machine M accepts a string w if thereexists a sequence of 1. For example, let us take three variable C1,C2,C3. C1 is the starting configuration of M on input w, 2. Cn is an accepting configuration, 3. for each 1 ≤ i < n, Ci yields Ci+1. L(M), language of M (the language recognized by M), is the set of strings
And here, set of strings is A(M)=1

Answer 3(b):
M = "On input string w:
1. Scan the tape and mark the first 0 which has not been marked. If no unmarked 0 is found, go to stage 4. Otherwise, move the head back to the front of the tape.
2. Scan the tape and mark the first 1 which has not been marked. If no unmarked 1 is found, reject
. 3. Move the head back to the front of the tape and go to stage 1.
4. Move the head back to the front of the tape. Scan the tape to see if any unmarked 1s remain. If none are found, accept; otherwise, reject."
After performing these algorithms if there is no strings for the relevant sizes given in question, then, it will come to default position .and it will print a default output as 1.

Answer 3(c):
in this part we adopt the following algorithm for proving as
M = "On input string is X(input):
1. Select the first input of G and mark it.
2. Repeat the following stage until no new similar iinput are marked:
3. For each input in x, make sure that all unique inputs are marked in q number of states are already marked.
4. Scan all the inputs of x to determine whether they all are marked. If they are,
accept; otherwise, reject."
For accept show 1 and for every rejection show 0.
So, C(M, x, q) =1 for all accepted values and for their relative spaces.

ENROL WITH NUMBERED SETS AND REDUCTIONS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES OF EXPERTSMINDS.COM AND GET BETTER RESULTS IN NUMBERED SETS AND REDUCTIONS ASSIGNMENTS!

Question 4:

Partial resolvability.Lets look at the problem MORTAL-MATRIX, where given matrices M1, ..., Mk and have to print answer 1, if a multiplication Mi1Mi2 ... Mim, can be created from these matrices. Multiplication equal to the matrix, where all the elements are equally with 0. Substantiate that MORTAL-MATRIX ir partial solved (algorithmically numbered

Answer:

Proof Let {M1,... , Mk} be a set of n x n integer matrices. Define two nm x nm matrices by A = diag(Mi,... , Mi) (i.e., A is block-diagonal with blocks M 1, , Mm in that order) and 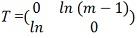where In is the n x n identity matrix. Notice that Tm = InmT^m=l_mnand Ak := T^(k-1)AT^(m-(k-m)) = T^(k-1)AT^(-(k-1)) = diag (Bk, ', B, B1, , B_(K-1)) for k = 1, ... , m. We claim that {B1,... ,Bmi} is partially resolve if and only if {A, T} is.

In order to prove our claim suppose first that Bi, ...Biq = 0 for some i_j belongs to {1,..., m}. Then, the first block of the block-diagonal matrix Ai, ' A(t+m) equal to zero.

But then ∏_(k=1)^(m-1)¦?T^k AT^(-(k-1)) ?= 0, k=O and sinCe this product can be written as a product of matrices in {A, T} the first implication is proved.

Suppose now that P :=T^t1AT^((t2))for some ti,and assume without loss of generality that 0 < ti < m - 1. We clearly have P = T^t1AT^t2 and for all other values of multiplicationwe can say that. By recursion we are thus lead to T = A_(ti+1)..........A_(ti+m) =0 .
for some t, > 0. The matrices Ak are block diagonal and the second implication is therefore proved.

So, by proving these two implications we can say that mortal matrix problem ffor matrix multiplication is partially resolvable .because if second implication is 0 the, we can easily fing the value of variables by equation it equal to zero.
and for every resolvable matrix it print 1 .

So as this problem is resolvable. It will print 1 as a result.

24/7 AVAILABILITY OF TRUSTED NUMBERED SETS AND REDUCTIONS ASSIGNMENT WRITERS! ORDER ASSIGNMENTS FOR BETTER RESULTS!