WORK TOGETHER WITH EXPERTSMIND'S TUTOR TO ACHIEVE SUCCESS IN HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT!
HA1011 Applied Quantitative Methods - Holmes Institute
LO1. Explain how statistical techniques can solve business problems
LO2. Identify and evaluate valid statistical techniques in a given scenario to solve business problems
LO3. Explain and justify the results of a statistical analysis in the context of critical reasoning for a business problem solving
LO4. Apply statistical knowledge to summarize data graphically and statistically, either manually or via a computer package
LO5. Justify and interpret statistical/analytical scenarios that best fits business solution
Statistical Analysis
Question: Construct a frequency distribution using 10 classes, stating the Frequency, Relative Frequency, Cumulative Relative Frequency and Class Midpoint
Answer:
a)
|
Class
|
Frequency
|
Relative Frequency
|
Cumulative Relative Frequency
|
Class Midpoint
|
|
0350
|
10
|
0.167
|
0.167
|
175
|
|
350650
|
16
|
0.267
|
0.43
|
500
|
|
650950
|
8
|
0.133
|
0.57
|
800
|
|
9501250
|
11
|
0.183
|
0.75
|
1100
|
|
12501550
|
4
|
0.067
|
0.82
|
1400
|
|
15501850
|
4
|
0.067
|
0.88
|
1700
|
|
18502150
|
2
|
0.033
|
0.92
|
2000
|
|
21502450
|
2
|
0.033
|
0.95
|
2300
|
|
24502750
|
1
|
0.017
|
0.97
|
2600
|
|
27503050
|
2
|
0.033
|
1.00
|
2900
|
|
Total
|
60
|
1.000
|
|
|
Question. b. Using (a), construct a histogram.
Answer: b)
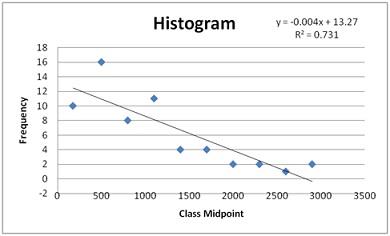
Question.c. Based upon the raw data (NOT the Frequency Distribution), what is the mean, median and mode?
Answer: c)
|
Mean
|
976.57
|
|
Median
|
797.50
|
|
Mode
|
401.00
|
SAVE DISTINCTION MARKS IN EACH HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT WHICH IS WRITTEN BY OUR PROFESSIONAL WRITER!
Answer 2
Question.a. Is above a population or a sample? Explain the difference.
Answer a)
Population contains all the features of the all the members of a specified group whereas sample data set includes only a subset of a population which means few features of some of the members can be presented by the sample (Gravetter, and Wallnau, 2007). In the given case, the manager of supermarket in Holmes Building provides sales data of chocolate bars sold for 7 weeks which is a sample because of containing only a subset and not the entire population of chocolate bars for whole period for the purpose.
Question.b. Calculate the standard deviation of the weekly attendance. Show your workings.
Answer b)
Standard deviation of Weekly attendance 74.06
Question.c. Calculate the Inter Quartile Range (IQR) of the chocolate bars sold. When is the IQR more useful than the standard deviation?
Answer c)
First quartile range 6114
Third quartile range 7216
Inter Quartile Range (IQR) 1102
The interquartile range is better than standard deviation in case the given data are not skewed or not have outliers (Lesik, 2018).
Question.d. Calculate the correlation coefficient. Using the problem we started with, interpret the correlation coefficient.
Answer d)
|
|
Weekly attendance
|
Number of chocolate bars sold
|
|
Weekly attendance
|
1
|
|
|
Number of chocolate bars sold
|
0.967993
|
1
|
Coefficient of correlation is 0.968 which shows positive strong relationship between the attendance and the number of chocolate bars sold. Both attendance and sale of chocolate bars are moving in the same direction. Increase in the students' attendance will increase the number of the chocolate bars sale (Gerver, and Sgroi, 2017).
Answer 3
|
SUMMARY OUTPUT
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Regression Statistics
|
|
|
|
|
|
|
Multiple R
|
0.967993
|
|
|
|
|
|
|
R Square
|
0.93701
|
|
|
|
|
|
|
Adjusted R Square
|
0.924412
|
|
|
|
|
|
|
Standard Error
|
224.5952
|
|
|
|
|
|
|
Observations
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANOVA
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Significance F
|
|
|
Regression
|
1
|
3751817
|
3751817
|
74.37736
|
0.000346
|
|
|
Residual
|
5
|
252215
|
50442.99
|
|
|
|
|
Total
|
6
|
4004032
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coefficients
|
Standard Error
|
t Stat
|
Pvalue
|
Lower 95%
|
Upper 95%
|
|
Intercept
|
1628.689
|
605.9
|
2.688049
|
0.0434
|
71.1734
|
3186.205
|
|
Weekly attendance
|
10.67723
|
1.238051
|
8.624231
|
0.000346
|
7.494724
|
13.85974
|
Question.a. Calculate AND interpret the Regression Equation. You are welcome to use Excel to check your calculations, but you must first do them by hand. Show your workings.
Answer a)
Regression Equation is given below:
Y = 10.67723*X + 1628.689
X = Attendance
For example, 10 student attendances are more, how much will be sale bards are given below:
Y = 10.67723*10 + 1628.689 = 1735.4613
10 students more attendance will increase chocolate bards by 1735.4613 more bars.
Question.b. Calculate AND interpret the Coefficient of Determination.
Answer b)
Coefficient of determination of the regression is 0.93701 which assurance high fitness of the regression model explains the variability of the independent variable through the dependent variable. The model can explain variability of students attendance up to 93.70% through the number of chocolate bars sale (Allen, 2007).
GET ASSURED A++ GRADE IN EACH HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT ORDER - ORDER FOR ORIGINALLY WRITTEN SOLUTIONS!
Answer 4
|
|
Scientific training
|
Grassroots training
|
Total
|
|
Recruited from Holmes students
|
35
|
92
|
127
|
|
External recruitment
|
54
|
12
|
66
|
|
Total
|
89
|
104
|
193
|
Question.a. What is the probability that a randomly chosen player will be from Holmes OR receiving Grassroots training?
Answer a)
127/193+104/193-92/193=0.72
The probability of randomly selecting a player from Holmes OR receiving Grassroots training will be 0.72.
Question.b. What is the probability that a randomly selected player will be External AND be in scientific training?
Answer b)
54/193=0.28
The probability of selecting randomly a player of External AND be in scientific training will be 0.28.
Question.c. Given that a player is from Holmes, what is the probability that he is in scientific training?
Answer c)
35/127=0.2755
Given that a player is from Holmes, the probability that he is in scientific training is 0.2755.
Question.d. Is training independent from recruitment? Show your calculations and then explain in your own words what it means.
Answer d)
Probability of selecting a player without considering recruitment = 1/89 + 1/104 = 0.021
Probability of selecting a player with considering training = 1/193 = 0.0052
Both the probability figures are different that reflects training is not independent from recruitment.
Answer 5
Question.A. The company would like to know the probably that a consumer comes from segment A if it is known that this consumer prefers Product X over Product Y and Product Z.
Answer a)
P(Prefers Product X over Product Y and Product Z) = 20%
P(Consumer from segment A) = 55%
P (Consumer comes from segment A if consumer prefers Product X over Product Y and Product Z) =
(20%)/(55%)=36.36%
SAVE YOUR HIGHER GRADE WITH ACQUIRING HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT HELP & QUALITY HOMEWORK WRITING SERVICES OF EXPERTSMINDS.COM
Question.B. Overall, what is the probability that a random consumer's first preference is product X?
Answer b)
P (consumer's first preference is product X) =
(55%×30%×10%×5%)/(20%)=41.25%
Answer 6
Question.A. During a 1 minute period you counted 8 people entering the store. What is the probability that only 2 or less of those 8 people will buy anything?
Answer a)
P (buy) = 1/8=0.125
P (buy) = 10.125 = 0.875
P(x)= n!/(n-x)!x!×?(p)?^x ?(q)?^((n-x)) (Laudanski, 2012)
P(0)
P(0)= 8!/(8-0)!0!×?(0.125)?^0 ?(0.875)?^((8-0))
P(0)= 8!/(8-0)!0!×?(0.125)?^0 ?(0.875)?^((8-0))
P(0)= 0
P(1)
P(1)= 8!/(8-1)!1!×?(0.125)?^1 ?(0.875)?^((8-1))
P(1)= 0.3927
P(2)
P(2)= 8!/(8-2)!2!×?(0.125)?^2 ?(0.875)?^((8-2))
P(2)= 0.1963
Probability of 2 or less than 2 customers buy = 0.3927 + 0.1963 = 0.589 = 58.90%.
Question.b) You need at least 6 staff members to help that many customers but usually have 7 staff on roster during that time slot. The 7th staff member rang to let you know he will be 2 minutes late. What is the probability 9 people will enter the store in the next 2 minutes?
Answer b)
P(k) = (e^(-λ) λ^k)/k!
P(9) = (?2.71828?^(-4) 4^9)/9!
P(9)= (?2.71828?^(-4) 4^9)/9!
P(9)=0.013231
The probability 9 people will enter the store in the next 2 minutes is 0.013231.
Average number of customers = (4+4)/2 = 4
EXPERTSMINDS.COM ACCEPTS INSTANT AND SHORT DEADLINES ORDER FOR HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT - ORDER TODAY FOR EXCELLENCE!
Answer 7
Question.A. Assuming a normal distribution, what is the probability that apartment will sell for over $2 million?
Answer a)
Average sale = µ = $1,100,000
Standard Deviation = σ = $385,000
X = $2,000,000
Z= (X-µ )/σ
Z= ($2,000,000-$1,100,000 )/$385,000
Z = 2.337
Probability figure at z = 2.337 is 0.9903.
The probability of apartment will be sold for over $2 million is 0.0097 (10.9903).
Question. B. What is the probability that the apartment will sell for over $1 million but less than $1.1 million?
Answer b)
Average sale = µ = $1,100,000
Standard Deviation = σ = $385,000
X = $1,000,000
Z= (X-µ )/σ
Z= ($1,000,000-$1,100,000 )/$385,000
Z = 0.26
Probability figure at z = 0.26 is 0.3975.
Average sale = µ = $1,100,000
Standard Deviation = σ = $385,000
X = $1,100,000
Z= (X-µ )/σ
Z= ($1,100,000-$1,100,000 )/$385,000
Z = 0
Probability figure at z = 0 is 0.5.
The probability of apartment will be sold for over $1 million but less than $1.1 million is 0.1025 (0.500.3975) (Browner, 2006).
GET GUARANTEED SATISFACTION OR MONEY BACK UNDER HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT HELP SERVICES OF EXPERTSMINDS.COM - ORDER TODAY NEW COPY OF THIS ASSIGNMENT!
Answer 8
Question. A. Since the apartments on Surfers Paradise are a mix of cheap older and more expensive new apartments, you know the distribution is NOT normal. Can you still use a Z-distribution to test your assistant's research findings against yours? Why, or why not?
Answer a)
Normal distribution data set is rare in the real world because of the slightly skewed data distribution. However highly skewed data distribution needs to find the outliers and after excluding the same, the data can be normalized for the statistical analysis. Skewed data rejects the mean as measure of central tendency. In this situation, Median can be taken as measure of central tendency. Therefore, in the given case, the given data distribution is not normally distribution, in this case also Zdistribution is used because there is use of the standard deviation for finding the value of the same (Gravetter, and Wallnau, 2009).
Question. Based on your sample of 45 investors, what is the probability that 30% of the investors would be willing to commit $1 million or more to the fund?
Answer b)
Average investment = µ = $950,000
Standard Deviation = σ = $385,000
X = $1,000,000
Z= (X-µ )/σ
Z= ($1,000,000-$950,000 )/$385,000
Z = 0.1299 = 0.13
Probability figure at z = 0.13 is 0.5517.
The probability that 30% of the investors will be willing to commit $1 million or more to the funds is 0.5517.
NEVER BE CAUGHT IN PLAGIARISM, AVAIL HA1011 APPLIED QUANTITATIVE METHODS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM AND SAVE HIGHER MARKS!
Listed below some of the major courses cover under our Holmes Institute Assignment Help Service:-
- HA1022 - Principles of Financial Management Assignment Help
- HA2022 - Business Law Assignment Help
- HA3011 - Advanced Financial Accounting Assignment Help
- HA3042 - Taxation Law Assignment Help
- HC2091 - Business Finance Assignment Help
- HC1072 - Economics & International Trade Assignment Help
- HA2032 - Corporate & Financial Accounting Assignment Help
- HA3021 - Corporations Law Assignment Help
- HC1010 - Accounting for Business Assignment Help