Assignment - Hydrostatic and Hydrodynamic Problems
Learning Outcomes -
Apply concepts of physics to develop solutions to hydrostatic and hydrodynamic problems.
Calculate forces related to fluids at rest and in motion.
Develop practical solutions for the distribution of fluids within correctly sized pipes.
Calculate the hydrostatic pressure exerted on substructures for a given context.
Design complex columns and piled foundations based on calculation.
ENROL WITH HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES OF EXPERTSMINDS.COM AND GET BETTER RESULTS IN HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENTS!
Question 1 - As an assistant engineer, calculate the friction loss of a fluid flow.
a. Plot the velocity distribution curve and determine the mean velocity of the flow and comment the flow condition and characteristics of the flow.
b. If the fluid flow is a turbulent flow, use a diagram or model to illustrate the flow.
c. From (a) and (b), compare the hydraulic conditions and highlight the merits of different solutions.
Answer - Apply concepts of physics
|
Distance from one plate (mm)
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
|
Velocity (m/s)
|
0
|
23
|
28
|
30
|
32
|
29
|
22
|
15
|
0
|
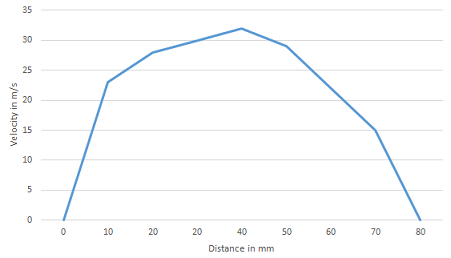
The average velocity u- = (0+23+28+30+32+29+22+15+0)/9 = 19.889 m/s
From the graph, the change in velocity per unit distance is approximately constant throughout the length. The motion of the flow is highly ordered. The velocity of the flow is also relatively slow. Thus the flow is laminar.
a)
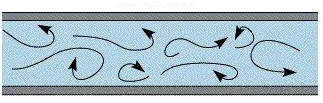
For a turbulent flow, eddies and waves results to unpredictable flow. The rate of flow is high and the viscosity low.
b) If the fluid remains non compressible and its viscosity remain constant, then its pressure drop would be:
Pressure drop dp/dx= (-2μumax)/H2
Where H is half the channel height = 0.001
dp/dx= (-2*0.001*32)/0.0012
= -64000 N/m3
= -64 KN/m2 per m
Wall shearing stress τ = -H dp/dx
τ = -0.001*(-64000)
= 64 N/m2
Laminar flow is smooth and less head is lost due to friction. It is characterised by high viscosity and relatively low velocity in a low characteristic linear dimensions.
Turbulent flow is associated with higher characteristic linear dimensions. The velocity of flow is high and thus high head is lost due to friction.
24/7 AVAILABILITY OF TRUSTED HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENT WRITERS! ORDER ASSIGNMENTS FOR BETTER RESULTS!
Question 2 - Calculate the following for the water discharge system so that the storm water can be properly discharged from the site.
a. Determine the friction factor with Darcy-Weisback equation for water flowing through a 300mm diameter pipe with water flow rate at 0.2m3/s and 120m long pipe run under a pressure difference of 3.8m head.
b. An open channel for storm water discharge system with a cross-section of trapezium shape with a bottom width of 4m and side slopes of 1 vertical to 1.5 horizontal. Assume the roughness coefficient n is 0.025, the bed slope is 1/1800 and the depth of the water is 1.2m. Determine the volume rate with Manning formula.
c. Discuss the calculation methodologies and hence discuss the differences and similarity for fluid flow in pipelines and open channels.
Answer - Calculate forces related to fluids at rest and in motion
a) Friction factor f= (hf2gD)/(Lv2)
Substituting the values
f = (3.8*2*9.81*0.3)/(120*(0.2/(π*0.152))2)
f = 0.0233
b) Manning's formula Q= (AR(2/3)S(1/2))/n
A = 1/2 (a+b)h
a = 4m
b = 4+2(1.5*1.2) = 7.6 m
Thus
A = 1/2 (4+7.6)*1.2 = 6.96 m2
Hydraulic radius R = A/P
P = 4+2(1.82 + 1.22)(1/2) = 8.327 m
Hence R = 6.96/8.327 = 0.8358
S = 1/1800
N = 0.025
Substituting back into the formula;
Q = (6.96*0.8358(2/3)*(1/1800)(1/2))/0.025
Q = 5.823 m3/s
The volume rate of the fluid is 5.823 m3/s.
Re = (ρ*v*Hydraulic Radius)/μ, v = Q/A
Re = (1000*5.823*0.8358)/(6.96*8.9x10-4)
Re = 785687.62 > 2000,
We can describe the flow as turbulent.
c) All methodologies employed in calculating the discharge of a channel yields same results because flow data used and parameters like friction coefficients are same in all cases. In pipelines, the flow is negligibly affected by environmental conditions and other external factors as compared to open channels like:
1. Speed and direction of wind effects open channel flow whereas wind has no effect on pipe flows.
2. Temperature and heat has direct effect on open channel flow. Pipe flows are somewhat insulated by pipe material. If pipe material is a good insulator, the fluid in pipe is affected very little.
3. External pressure of air impacts directly on open channel flows. Whereas external pressure and stresses are first bear by elasticity of pipe before affecting flow.
4. Pipe flows are very much secured from disturbances unlike open channels which are too much exposed.
GET ASSURED A++ GRADE IN EACH HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENT ORDER - ORDER FOR ORIGINALLY WRITTEN SOLUTIONS!
Question 3 - You are being asked by your supervisor to analysis the fluid flow of a pipeline.
a. Water is flowing through a 40mm diameter pipe with an average velocity of 0.1m/s. You are required to identify the condition of flow and calculate the head loss of the fluid under that flow condition. Assume the density and viscosity of water are 998kg/m3 and 1.002x103 Ns/m2.
b. To control the flow to be laminar flow, what is the pipe size for the fluid flow?
c. From the results above or otherwise, evaluate the flow conditions would occur under different pipe sizes.
d. Determine and give comment the pipe sizes and the characteristic of fluid for the efficiency of the fluid flow in a pipe.
Answer -
a) Reynolds number Re= ρVD/μ
Substituting back the values we have
Re = (998*0.1*0.04)/(1.002*10-3)
= 3992 > 2000
Since the Reynold's number is greater than 2000, the flow is turbulent.
Assuming the pipe material to be forged steel, ε = 0.025 mm.
Using Colebrook's equation to find friction factor,
f=1.325/(ln(5.74/Re0.9 + (ε/D)/3.7))2
f = 0.0413
Using Darcy-Weisbach's equation, for unit length of pipe, the head loss is:
hf = (fLv2)/2gD
hf = 5.262 x 10-4 m
hf = 0.526 mm
b) Reynold's number for laminar flow should be less than 2000, Say 1999. We will have
1999 = (998*0.1*D)/(1.002*10-3)
D = 0.02007 m ≈ 20 mm
c) From (a) and (b) above, when the diameter was reduced from 40 mm to 20 mm, the flow changed from turbulent to laminar.
For Diameter = 20 mm,
r = 10 x10-3 m
Flow rate = Q = πr2*v
Q = 3.14*10x10-3 * 0.1
Q = 3.1416x10-3 m3/s
For Diameter = 40 mm,
r = 20 x10-3 m
Q = 3.14*20x10-3 * 0.1
Q = 6.2832x10-3 m3/s
This means that when the diameter is increased, the flow rate increases and its viscosity become low.
d) From the values obtained in (a) and (b) above, we explain as follows.
For D = 40 mm, Re = (998*0.1*0.04)/(1.002*10-3)
= 3992 > 2000
For D = 20 mm
Re = (998*0.1*0.02)/(1.002*10-3)
= 1999 < 2000
In this case, we reduced the diameter to 20 mm. Increasing the diameter leads to a higher Reynolds number making the flow turbulent. Turbulent flow has higher frictional losses as compared to laminar flow.
Efficiency = 1999/3992* 100 = 50.075%
The efficiency of pipe is nearly 50%. It shows that efficiency of pipe is reduced to half due to friction losses.
NO PLAGIARISM POLICY - ORDER NEW HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENT & GET WELL WRITTEN SOLUTIONS DOCUMENTS WITH FREE TURNTIN REPORT!
Question 4 - As being an engineer for a project
a. Calculate the pressure exerting on the vertical wall.
b. Calculate the pressure exerting on the horizontal floor surface.
c. From the result of (a) & (b), calculate the force acting on the structural elements and comment on the ability of the structural element to resist the force exerted by the groundwater.
d. Explain with proposals how the structural elements to be improved to resist the external hydrostatic pressure.
Answer -
a) Pressure exerted on the vertical wall.
weight acting on the bottom floor F=volume*unit weight
F = (5*12*3)*1 = 180 N
Thus, pressure acting on the wall
P = (1/2*F*h)/bh
= (1/2*180*3)/(10*4)=6.75 N/m2
b) Pressure exerted on horizontal surface = F/A
= 180/(10*5)
= 3.6 N/mm2
c) Force acting on the structure = (6.75*(10*4)) + (3.6*(10*5))
= 450 N
The structure is capable of resisting force exerted by the ground water. This is possible because the pressure on the horizontal surface is lower than that on the vertical wall. This means that the structure cannot overturn.
d)
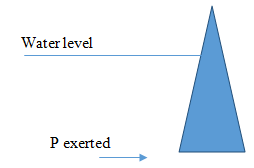
To resist external hydrostatic pressure, the vertical wall should be in the shape of trapezoid with a wide base and a narrow top. This prevents toppling over in cases when external pressure is exerted on the wall.
ENDLESS SUPPORT IN HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENTS WRITING SERVICES - YOU GET REVISED OR MODIFIED WORK TILL YOU ARE SATISFIED WITH OUR HYDROSTATIC AND HYDRODYNAMIC ASSIGNMENT HELP SERVICES!