Basic Concepts of Matrices

A rectangular array of numbers and functions in an ordered form is known as Matrix, where numbers and functions are known as components of the matrix. 

Let us suppose you have 5 iPhones and 10 Samsung Tablets(You are a rich man!), you can express it as [5 10] knowing that the number inside represents iPhones and Tablets. Now I have 3 iPhones and 6 Samsung Tablets ( I am also rich but not as rich as you), I can also express it as [3 6]. Now, both of these data can be transformed and expressed as follows:

A =  | 5 10 |

       | 3  6  |

In this arrangement 5 10 represents the first row, 3 6 represents the second row, 5 3 represents the first column and 10 6 represents the second column. The first column represents a number of iPhones possessed by you and I and second column represent a number of Samsung tablets possessed by us.

The given example above is a matrix. Matrices are denoted by capital letters like in this case. The horizontal lines of elements represent the row of the matrix and vertical lines of elements represent columns of the matrix. Here A has 2 rows and 2 columns. This is also known as Square Matrix which you will study below.

Order of Matrix:

The matrix consists of rows and columns. In the above example we saw Matrix A has 2 rows and 2 columns, thus an order of matrix is 2*2. Generally, the matrix consisting of x rows and y columns is read out as a matrix of order m*n or m*n matrix.

Generally, m*n matrix has following rectangular arrangement: 

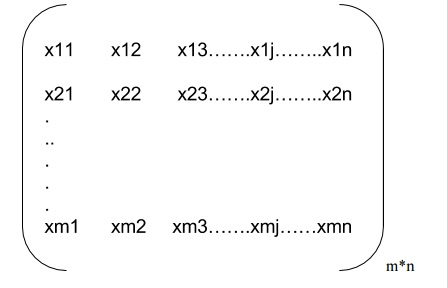
X = [x_ij ]_m*n where 1=< i =< m, 1=< j =< n

Types of Matrices:

Column Matrix: Matrix with one column is known as Column Matrix. It is represented as X = [x_ij ]_m*1,matrix of order m * 1. 

Row Matrix?: Matrix with one row is known as Row Matrix. It is represented as X = [x_ij ]_1*n, matrix of order 1 * n. 

Square Matrix?: Matrix with an equal number of rows and columns is known as Square Matrix i.e. when rows m = columns n. It is represented as X = [x_ij ]_m*m,matrix of order m. 

Diagonal Matrix: When all non-diagonal elements of a matrix become zero, it is known as Diagonal Matrix. Matrix X = [x_ij ]_m*m is called a diagonal matrix if x_ij = 0 when i ≠ j.

Scalar Matrix: When diagonal elements of a diagonal matrix becomes equal, it is known as Scalar Matrix. Matrix X = [x_ij ]_m*m is called a scalar matrix if x_ij = 0, when i ≠ j, x_ij = k, when i = j, for constant k. 

Identity Matrix : When diagonal elements are 1 and rest are all zero it is known as Identity Matrix. Matrix X = [x_ij ]_m*m is an identity matrix, if x_ij = 1 for i =j and if x_ij = 0 for i ≠ j. 

Zero Matrix: When all elements of a matrix are zero it is known as zero matrix.

Note: Two matrices X = [x_ij ] and Y = [y_ij ] are equal if they are of same order and each element of X and Y i.e.x_ij = y_ij for all i = j.  

Operations on Matrices: 

Addition of Matrices: Matrices can only be added when they are of same order. Suppose we have matrix A & B, both of order 2*2. The sum of matrices A and B is denoted by C.

Thus sum of two matrices A = [a_ij ] and B = [b_ij ] is defined as matrix C = [c_ij ]_m*n , where c_ij = a_ij+ b_ij for all values of i and j.  

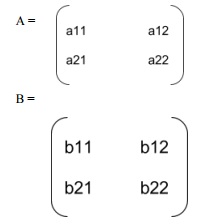
Subtraction of Matrices?: Matrices can only be subtracted when they are of same order. Difference of two matrices A = [a_ij ] and B = [b_ij ] is defined as matrix C = [c_ij ]_m*n , where c_ij = a_ij - b_ij for all values of i and j. 

Properties of Addition of Matrices: 

1) Commutative Law: If matrices A and B are of same order, then A+B = B+A

2) Associative Law: If matrices A and B and C are of same order then (A + B) + C = A + (B +C)

Multiplication of Matrices: For multiplication of matrices number of columns in one matrix should be equal to the number of rows in another matrix i.e. number of columns in matrix X is equal to the number of rows in matrix Y. If X = [x_ij ]_m*n and Y = [y_jk ] _n*p then product of two matrices X and Y is the matrix Z of order m*p i.e. Z = [z_ik ]_m*p  

Properties of Multiplication of Matrices: 

1) Associative Law: For matrices X, Y and Z, (XY)Z = X(YZ)

2) Distributive Law: For matrices X, Y and Z , X(Y+Z) = XY + XZ or (X+Y)Z = XZ + YZ 

Transpose of a Matrix: For matrix A = [a_ij ]_m*n ,the matrix obtained by interchanging the rows and columns of A is called transpose of A, denoted by AT .

Importance of Matrices:

Matrices are very useful in the field of science as well as find applications in practical problems of real life, thus it is a requisite concept. Considering it as an important tool in mathematics, it simplifies our work to great extent as compared to other methods used in mathematics. Operations and notations of matrix are used in electronic spreadsheets, electrical circuits(for example solving questions of Kirchoff’s laws), in field of optics and quantum mechanics, in areas of business and science for cost estimation, budgeting, projection of sales, for seismic survey in the field of geology, robotics and automation concept of matrices plays an active role. Matrices play a vital role in computer-based applications, it is used for the projection of 3D image into a 2D screen, thus generating motions which seem realistic.

How we help you? - Matrices-Matrix Algebra Assignment Help 24x7

We offer Matrices-Matrix Algebra assignment help, math assignment writing help, assessments writing service,math tutors support, step by step solutions to Matrices-Matrix Algebra problems, Matrices-Matrix Algebra answers, math assignment experts help online. Our math assignment help service is most popular and browsed all over the world for each grade level.

There are key services in math which are listed below:-

• Matrices-Matrix Algebra help
• Assignment Help
• Homework Help
• Matrices-Matrix Algebra Assessments Writing Service
• Solutions to problems
• math Experts support 24x7
• Online tutoring

Why choose us - The first thing come in your mind that why choose us why not others what is special and different about us in comparison to other site. As we told you our team of expert, they are best in their field and we are always live to help you in your assignment which makes it special.

Key features of services are listed below:

• Confidentiality of student private information
• 100% unique and original solutions
• Step by step explanations of problems
• Minimum 4 minutes turnaround time - fast and reliable service
• Secure payment options
• On time delivery
• Unlimited clarification till you are done
• Guaranteed satisfaction
• Affordable price to cover maximum number of students in service
• Easy and powerful interface to track your order