Basic Concepts of Determinants:

To every square matrix X = [x_ij]_n*n of order n, a real or complex number can be associated which is known as the determinant of that square matrix, where x_ij = (i, j)^th  element of X. It is believed to be a function which associates a unique number with a square matrix. Let us say X is the set of square matrices, Y is the set of real or complex numbers and f:X→Y is defined by f(R) = y, where R ∈ X and y ∈ Y, then we call f(R) as the determinant of R. It is denoted by det R or l R l .

If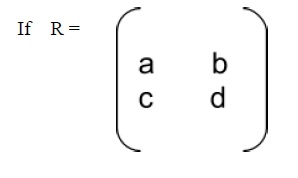    

Then determinant of R is written as det R = 

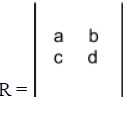
Note: | R | is read as determinant R for matrix R and not as modulus of R.

           Determinants exists only for square matrices.

Determinants of Matrix of order one:  If R = [r] is the matrix of order 1, then determinant is equal to r for matrix R.

Determinants of Matrix of order two:

If  R is a

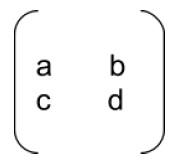
matrix of order 2*2

Then determinant of a matrix R is defined as det ( R) = ad - cb

Determinants of Matrix of order three:  For a matrix of order 3*3 , determinant is defined by expressing it in terms of determinant of second order which is also known as expansion of determinant along rows and columns which can be done in 6 possible ways i.e 3 corresponding for each rows and 3 corresponding for each columns.

Note: To make the calculation easier usually determinant expansion is done along that row or column which has maximum number of zeroes. 

Adjoint of a Matrix: Adjoint of a square matrix X = [x_ij]_n*n  is defined as the transpose of the matrix [x_ij]_n*n where x_ij element as the cofactor X_ij.

Properties of Determinants: 

1.      On interchanging the rows and columns of a determinant, its value remains unchanged. For a square matrix X, det(X) = det(X') where X' is transpose of X.

2.      On interchanging any two rows or columns of a determinant, sign of determinant changes.

3.      For two identical rows or columns, the value of determinant is zero.

4.      On multiplying each row and column of a determinant with constant k, value of a determinant gets multiplied by k.

5.      When some or all elements of a row or column of determinant are written as sum of two or more terms, then determinant is also written as sum of two or more determinants.

6.      Multiplying a determinant by k means that elements of only one row or column is multiplied by k.

7.      If X = [x_ij]_3*3, then | k. R | = k^{3 |} R |

8.      When equimultiples of a corresponding elements of other rows or columns is added to each element of rows and columns of a determinant, then value of each determinant remains same.

9.      Minor of an element x_ij of the determinant of matrix X is denoted by M_ij and is the determinant determined by deleting i^th  row and j^th column.

10.  Cofactor of x_ij is given by X_ij = (-1)^i+j M_ij

11.  The value of determinant of matrix X is determined by the sum of products of elements of a row or column with corresponding factors determines

12.  On multiplying elements of one row or column with cofactors of elements of any other row or column, the resultant sum is zero.

13.  X(adj X) = (adj X) X = | X| I, where X is the square matrix of order n, adj X is the adjoint of matrix X also known as transpose of matrix X.

14.  Matrix X of order 2*2 is said to be singular or non-singular according as  | X | = 0 or 

           | X | ≠ 0.

Importance of Determinants: 

On the off chance that you ever wind up utilising math to take care of issues with a huge arrangement of autonomous yet connected, amounts, you frequently utilise direct variable based math to discover a wide range of arrangements, either correct or rough. On the off chance that you wind up doing any measure of the straight variable based math whatsoever, you will definitely need to discover the determinant of a lattice sooner or later, with a specific end goal to reverse it, discover its eigenvalues, or more outlandish issues.

So, determinants can appear in any field which can take care of issues with (a) a considerable measure of factors which (b) connect definitively. This is for all intents and purposes all of the science, designing, huge information, information investigation, business math, etc. Not everyone who takes a shot at those things needs determinants, however many individuals in those fields have absolutely utilised determinants. Cramer's Rule, named after Gabriel Cramer (1704-1752), utilises determinants to unravel the arrangement of direct conditions in factors. This control applies just to frameworks with remarkable arrangements.

Expertsminds.com offers Determinants Assignment Help, Determinants Assignment Writing Help, Determinants Assignment Tutors, Determinants Solutions, Determinants Answers, Mathematics Assignment Experts Online

How we help you? - Determinants Math Assignment Help 24x7

We offer Determinants  assignment help, Determinants assignment writing help, math assessments writing service, math tutors support, step by step solutions to Determinants problems, Determinants answers, math assignment experts help online. Our math assignment help service is most popular and browsed all over the world for each grade level.

There are key services in Determinants - Math which are listed below:-

• Determinants math help
• Assignment Help
• Homework Help
• Determinants Math Assessments Writing Service
• Solutions to Determinants math problems
• Experts support 24x7
• Online tutoring

Why choose us - The first thing come in your mind that why choose us why not others what is special and different about us in comparison to other site. As we told you our team of expert, they are best in their field and we are always live to help you in your assignment which makes it special.

Key features of services are listed below:

• Confidentiality of student private information
• 100% unique and original solutions
• Step by step explanations of problems
• Minimum 4 minutes turnaround time - fast and reliable service
• Secure payment options
• On time delivery
• Unlimited clarification till you are done
• Guaranteed satisfaction
• Affordable price to cover maximum number of students in service
• Easy and powerful interface to track your order