GET READYMADE CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT SOLUTIONS - 100% PLAGIARISM FREE WORK DOCUMENT AT NOMINAL CHARGES!

CP5602 - Advanced Algorithm Analysis Assignment - James Cook University, Australia

Q1. For a tree T, let n_I denote the number of its internal nodes, and let n_E denote the number of its external nodes. Show that if every internal node in T has exactly 3 children, then n_E = 2nI + 1.

Solution - Given that

n_l = Number of Internal Nodes for a tree T.

n_E = Number of External Nodes for a tree T.

To prove that, if every internal node has exactly 3 children then, 2n_E = 2n_l + 1

Let us check the values when n_l = 0

n_E = 2n_l + 1 = 2*0 + 1 = 1

Again, check the values when n_l = 1

n_E = 2n_l + 1 = 2*1 + 1 = 3

On generalizing the above equation for k values, we get

when n_l = k, then

n_E = 2n_l + 1 = 2(k-1) +1 + (3-1)

Therefore, 2k - 2 + 1 + 2

Hence, n_E = 2k + 1

From the above calculation it is clear that external nodes n_E is the equal to the number of external node when the value of n_E = K-1 as internal nodes.

MOST RELIABLE AND TRUSTWORTHY CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT HELP & HOMEWORK WRITING SERVICES AT YOUR DOORSTEPS!

Q2. Insert entries with keys, 2, 7, 3, 12, 5, 20, 14, 6, 11, 8, 15, 17, 1, 19, 23, 14 (in this order), into an empty:

(a) heap.

(b) binary search tree.

(c) AVL tree.

(d) (2, 4) tree.

a. Heap (Min Heap)

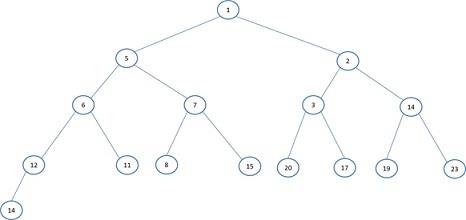
b. Binary Search Tree

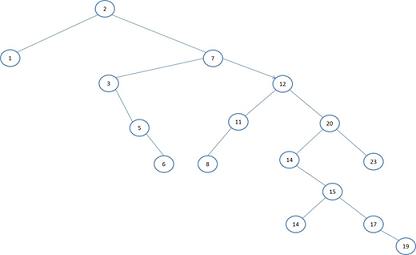
c. AVL

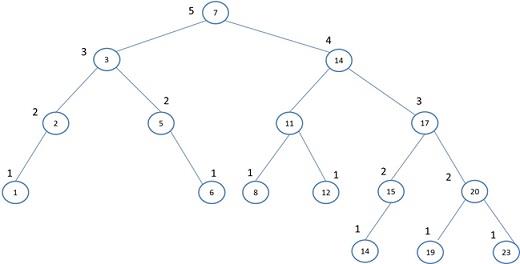
d. (2, 4) Tree

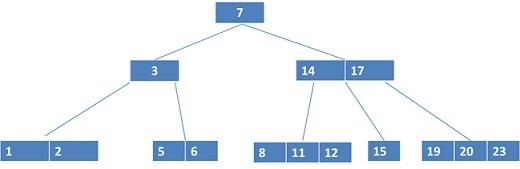
Q3. Although merge sort runs in θ(n lg n) worst-case time and insertion sort runs in θ(n²) worst case time, the constant factors in insertion sort make it faster for small n. Thus, it makes sense to use insertion sort within merge sort when sub problems become sufficiently small. Consider a modification to merge sort in which n/k sub lists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined.

i. Show that the n/k sub lists, each of length k, can be sorted by insertion sort in θ(nk) worst-case time.

Solution: Consider, if for the input size of k elements the worst case time complexity of insertion sort is O(k²).

Hence, the quadratic equation for calculating this running time is of type (ak² + bk + c).

Now, if the list is divided into multiple sub-lists i.e. n/m, each of length m. Then the insertion sort time complexity can be calculated from the recurrence relation as shown below.

T(k) = n/k (am² + bk + c)

T(k) = ank + bn + cn/k

Let us suppose, m is a very small integer having a negligible value as compared to that of n. In that case we can easily ignore the parameter m from the above equation.

Therefore,

T(k) = ank

Hence, the complexity of algorithms becomes O(nk).

SAVE DISTINCTION MARKS IN EACH CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT WHICH IS WRITTEN BY OUR PROFESSIONAL WRITER!

ii. Show that the sub-lists can be merged in θ(n lg(n/k)) worst-case time.

Let us assume that we have total n elements, which are divided into n/k sub-lists. All the n.k sub-lists are already sorted.

In order to merge all the sub-lists into a single list then following procedure has to be followed.

Consider any two sub-lists at a time and merge them using the merge sort. This will give another sub-list. The same process is continued until all the sub-lists are merged to form a single list of n elements.

The merge sort algorithms takes the time on order of O(log(n/k)) to merge the two sorted sub-lists.

For every sub-list the total n elements will be considered. So the total time complexity of merging the n/k sub-lists is O(nlog(n/k)).

iii. Given that the modified algorithm runs in θ(nk + n lg(n/k)) worst-case time, what is the largest asymptotic (θ-notation) value of k as a function of n for which the modified algorithm has the same asymptotic running time as standard merge sort.

In case of the new algorithm, given that it runs in the worst case time of the order (nk + n log(n/k)). To find the largest value of k, for which the new algorithm will show the same running time complexity as that of merge sort.

Given running time complexity of new algorithm is (nk + n log(n/k))

Can be re-written as (nk + n (log(n) - log(k))

Or, (nk + nlog(n) - nlog(k) ...........................................Equation 1

We have to prove that Equation 1 must be same as the running time of merge sort i.e. Θ(nlogn).

Assume k = Θ(log n), and replace the value of k in Equation 1

(nk + n log(n) - n log(k) = θ(n log (n) + n log(n) - n log(log n)) = (2n log (n) - n log(log n)) .....................................Equation 2

From Equation 2, we can say that the value of log(log(n)) is very small as compared to log n.

Therefore, by the ignoring the second term, the running time complexity from Equation 2 can be deduced to (2n log (n), where 2 is an constant value.

So, finally the running time complexity is of the order of (n log (n), which is nothing but the complexity of traditional merge sort algorithm.

HIRE PROFESSIONAL WRITER FROM EXPERTSMINDS.COM AND GET BEST QUALITY CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES!

Q4. Consider the recurrence T(n) = 3T(⌊n/2⌋) + n.

i. Use the master method to give tight asymptotic bound for this recurrence (if the master method cannot be used, explain why).

Solution: The given recurrence relation can be solved using the master theorem. Let us first discuss the statement of Masters Theorem.

The Masters theorem can be applied on the recurrence relation on the following recurrence pattern.

T(n) = aT(n/b) + f(n)

Where, a, b are constants having value greater than 1 and f(n) is any function of n. If this conditions hold, then there are three different cases that may occur.

Case 1: if f(n) = O(n^log_(b)a-€), where € is some constant value greater than 0.

Then,

T(n) = Θ(n^log_(b)a)

Case 2: if f(n) = Θ(n^log_(b)a log^kn) , where k is greater than equal to 1,

Then,

T(n) = Θ(n^log_(b)a log^k+1n)

Case 3: if f(n) = ?(n^log_(b)a+€), where € is some constant value greater than 0 and f(n) is some regular function of n.

Then

T(n) = Θ(f(n)).

Now the given recurrence relation is as below.

T(n) = 3T(⌊n/2⌋) + n

On comparing the above relation with the three different cases discussed above, we get that it gets matches with the case 1.

T(n) = aT(n/b) +f(n)

a = 3, b = 2, f(n) = n

Therefore according the rule of case 1,

T(n) = Θ(n^log3)

WE HELP STUDENTS TO IMPROVE THEIR GRADES! AVAIL TOP QUALITY CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES AT CHEAPER RATE!

ii. Use a recursion tree to determine a good asymptotic upper bound on this recurrence.

Given recurrence relation = T(n) = 3T(⌊n/2⌋) + n.

Let us assume for n integers, the recursion tree can be drawn as shown below,

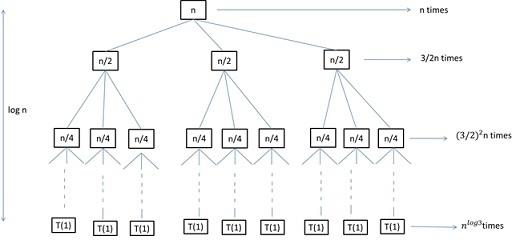
The given question when solved using the recurrence tree, we can see that the problem gets decreased by 2 every time the level of the tree is changing and ultimately reaching to the constant T(1).

Now, we can also analyze that at every level of the tree there are 3 extra nodes. Then the number of nodes at i^th level will be 3ⁱ. Because the size of the tree is decreasing every level by the factor of n/2 and at every level there are nodes. On adding all the levels we get the series as shown below,

T(n) = n + 3/2n + (3/2)^2n + -------------+ (3/2)^ (log n-1)n + Θ(n^log3)

Finding the summation of all the terms will give us the following series

= _k=0∑^logn-1 ((3/2)^k n + Θ(n^log3))

= (((B/2)^logn-1)/((3/2)-1))n + Θ(nl^og3)

= 2(n^log3) - 2n + Θ(n^log3)

= O(n^log3)

Hence Proved

iii. Use the substitution method to verify your answer.

Given recurrence = T(n) = 3T(⌊n/2⌋) + n.

Suppose k € Z, and k >=1 and Z is between 1<= i <=k

Consider a hypothetical solution as T(i) <= ai^log3)-cn

Assume T(k+1):

T(k+1) = 3T((k+1)/2) + k + 1

Substitute the value of T(i) in above equation, we get

T(k+1) <= 3a((k+1)/2)^log3 - 3/2c((k+1) + k+1

<= 3/2^log3a (k+1)^log3  - 3/2c((k+1) + k+1

<= a(k+1)^log3 - 3/2c((k+1) + k+1

<= a(k+1)^log3 - c(k+1)

Hence, the assumption we made earlier is true.

So, by the method of substitution, P(n) is true, for a = 3 , c = 2

NEVER MISS YOUR CHANCE TO EXCEL IN CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT! AVAIL AFFORDABLE AND RELIABLE CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENTS HELP SERVICES OF EXPERTSMINDS.COM!

Q5. Show all the steps for performing any of the following algorithms for matching the pattern 'rithm' in the text 'advancedalgorithmanalysis'.

(a) Boyer-Moore

Solution - a. Boyer-Moore

Given string text: advancedalgorithmanalysis

Pattern: rithm

Step 1: In the given string text, try to match the first 'm' characters

advancedalgorithmanalysis

This step is failed, shift to the next position i.e. after the index which was checked in the previous step.

Step 2: Try to match the given pattern from the index where the previous index was found un-matched.

advancedalgorithmanalysis

This step is also failed, shift to the next position i.e. after the index which was checked in the previous step.

Step 3: Try to match the given pattern from the index where the previous index was found un-matched.

advancedalgorithmanalysis

Here in this step some part of the string is matched. However the complete pattern matching fails. So in the next step, slide only up to the index which is matching with the given pattern.

Step 4: The first character that matches with the given pattern is the index of character 'r'. From the index of 'r' match the given string of 'm' characters.

advancedalgorithmanalysis

Finally, the given pattern is matched in the string text.

ENDLESS SUPPORT IN CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENTS WRITING SERVICES - YOU GET REVISED OR MODIFIED WORK TILL YOU ARE SATISFIED WITH OUR CP5602 - ADVANCED ALGORITHM ANALYSIS ASSIGNMENT HELP SERVICES!

Avail the James Cook University, Australia Assignment Help Services for related units and courses such as:-

• CP1403 - Design Thinking Assignment Help
• CP3103 - Independent Project Assignment Help
• CP1802 - Internet Fundamentals Assignment Help
• CP1402 - Internet Fundamentals Assignment Help
• CP3102 - Multidisciplinary Project Assignment Help
• CP1406 - Web Design and Development Assignment Help
• CP3402 - Content Management Systems Assignment Help
• CP3000 - Research Topics in Technology Assignment Help
• CP2412 - Game Design and Technologies Assignment Help
• CP3413 - Information Processing and Visualisation Assignment Help
• CP3405 - Design Thinking and Project Management Assignment Help
• CP1407 - Introductory Machine Learning and Data Science Assignment Help